
【題目】如圖,一次函數y=﹣x+4的圖象與反比例函數y=![]() (k為常數,且k≠0)的圖象交于A(1,a),B兩點.
(k為常數,且k≠0)的圖象交于A(1,a),B兩點.
(1)求反比例函數的表達式及點B的坐標;
(2)在x軸上找一點P,使PA+PB的值最小,求滿足條件的點P的坐標及△PAB的面積.

【答案】(1)反比例函數的表達式y=![]() ,點B的坐標為(3,1).(2)
,點B的坐標為(3,1).(2)![]() .
.
【解析】試題分析:(1)由點A在一次函數圖象上,結合一次函數解析式可求出點A的坐標,再由點A的坐標利用待定系數法即可求出反比例函數解析式,聯立兩函數解析式成方程組,解方程組即可求出點B坐標;
(2)作點B作關于x軸的對稱點D,交x軸于點C,連接AD,交x軸于點P,連接PB.由點B、D的對稱性結合點B的坐標找出點D的坐標,設直線AD的解析式為y=mx+n,結合點A、D的坐標利用待定系數法求出直線AD的解析式,令直線AD的解析式中y=0求出點P的坐標,再通過分割圖形結合三角形的面積公式即可得出結論.
試題解析:(1)把點A(1,a)代入一次函數y=-x+4,
得:a=-1+4,解得:a=3,
∴點A的坐標為(1,3).
把點A(1,3)代入反比例函數y=![]() ,
,
得:3=k,
∴反比例函數的表達式y=![]() ,
,
聯立兩個函數關系式成方程組得: 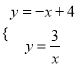 ,
,
解得: ![]() ,或
,或![]() ,
,
∴點B的坐標為(3,1).
(2)作點B作關于x軸的對稱點D,交x軸于點C,連接AD,交x軸于點P,此時PA+PB的值最小,連接PB,如圖所示.
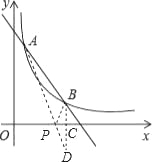
∵點B、D關于x軸對稱,點B的坐標為(3,1),
∴點D的坐標為(3,- 1).
設直線AD的解析式為y=mx+n,
把A,D兩點代入得: ![]() ,
,
解得: ![]() ,
,
∴直線AD的解析式為y=-2x+5.
令y=-2x+5中y=0,則-2x+5=0,
解得:x=![]() ,
,
∴點P的坐標為(![]() ,0).
,0).
S△PAB=S△ABD-S△PBD=![]() BD(xB-xA)-
BD(xB-xA)-![]() BD(xB-xP)
BD(xB-xP)
=![]() ×[1-(-1)]×(3-1)-
×[1-(-1)]×(3-1)-![]() ×[1-(-1)]×(3-
×[1-(-1)]×(3-![]() )
)
=![]() .
.


科目:初中數學 來源: 題型:
【題目】小麗剪了一些直角三角形紙片,她取出其中的幾張進行了如下的操作:
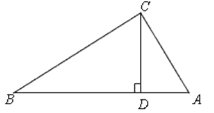
操作一:如圖,將Rt△ABC沿某條直線折疊,使斜邊的兩個端點A與B重合,折痕為DE.
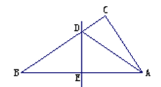
(1)如果AC=6cm,BC=8cm,試求△ACD的周長.
(2)如果∠CAD:∠BAD=4:7,求∠B的度數.
操作二:如圖,小麗拿出另一張Rt△ABC紙片,將直角邊AC沿直線AD折疊,使它落在斜邊AB上,且與AE重合,已知兩直角邊AC=6cm,BC=8cm,你能求出CD的長嗎?
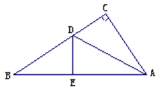
操作三:如圖,小麗又拿出另一張Rt△ABC紙片,將紙片折疊,折痕CD⊥AB。你能證明:BC2+AD2=AC2+BD2嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校9月的水費為![]() 元,電費比水費的2倍多40元,10月的水費比9月多支出了25%,電費比9月節約了25%.
元,電費比水費的2倍多40元,10月的水費比9月多支出了25%,電費比9月節約了25%.
(1)用![]() 表示該校9月的電費是多少元?
表示該校9月的電費是多少元?
(2)用![]() 表示該校10月的水、電費各是多少元?
表示該校10月的水、電費各是多少元?
(3)如果該校10月的水、電費共1130元,那么10月的水電費與9月相比超支或節約了多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若有![]() 兩個數,滿足關系式
兩個數,滿足關系式![]() ,則稱
,則稱![]() 為“共生數對",記作
為“共生數對",記作![]() .
.
例如:當2, 3滿足![]() 時,則(2, 3)是“共生數對".
時,則(2, 3)是“共生數對".
(1)若![]() 是“共生數對",求
是“共生數對",求![]() 的值:
的值:
(2)若![]() 是“共生數對“,判斷
是“共生數對“,判斷![]() 是否也是“共生數對",請通過計算說明:
是否也是“共生數對",請通過計算說明:
(3)請再寫出兩個不同的“共生數對”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A的坐標是(0,3),點B的坐標是(-4,0).
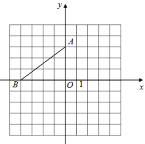
(1)畫出△AOB繞點A逆時針旋轉90°后得到的圖形△A1O1B1;并寫出點B1的坐標 ;
(2)畫出△AOB關于點P(0,-1)的中心對稱圖形△A2O2B2,并寫出點B2的坐標 ;
(3)若點Q為x軸上的一點,當B1Q+B2 Q的和最小時,直接寫出點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】重慶格力廠為了檢驗甲、乙兩車間生產的同一款新產品的合格情況(尺寸r的范圍為176≤r≤185的產品為合格),隨機各抽取了20個樣品進行檢測,過程如下:
收集數據(單位:mm)
甲車間:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙車間:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理數據
級別 頻數 | 165.5~ 170.5 | 170.5~ 175.5 | 175.5~ 180.5 | 180.5~ 185.5 | 185.5 ~190.5 | 190.5~ 195.5 |
甲車間 | 2 | 4 | a | b | 2 | 1 |
乙車間 | 1 | 2 | 9 | 6 | 2 | 0 |
分析數據:
車間 | 平均數 | 眾數 | 中位數 | 方差 |
甲車間 | 180 | 185 | 180 | 43.1 |
乙車間 | 180 | 180 | c | 22.6 |
應用數據
(2)請寫出表中a= ,b= ,c= mm.
(2)估計甲車間生產的1000個該款新產品中合格產品有多少個?
(3)結合上述數據信息,請判斷哪個車間生產的新產品更好,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
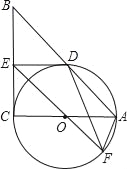
【題目】如圖,在Rt△ABC中,∠C=90°,以AC為直徑作⊙O,交AB于D,過點O作OE∥AB,交BC于E.
(1)求證:ED為⊙O的切線;
(2)若⊙O的半徑為3,ED=4,EO的延長線交⊙O于F,連DF、AF,求△ADF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機小張某天上午營運全是在東西走向的政府大道上進行的,如果規定向東為正,向西為負,他這天上午的行程是(單位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)將最后一名乘客送達目的地時,小張距上午出發點的距離是多少千米?在出發點的什么方向?
(2)若汽車耗油量為0.6升/千米,出車時,郵箱有油72.2升,若小張將最后一名乘客送達目的地,再返回出發地,問小張今天上午是否需要加油?若要加油至少需要加多少才能返回出發地?若不用加油,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
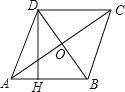
【題目】如圖,四邊形ABCD是菱形,對角線AC和BD相交于點O,AC=8cm,BD=6cm,DH⊥AB于H.
(1)求菱形ABCD的面積;
(2)求DH的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com