
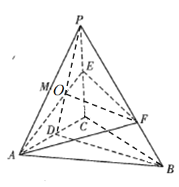
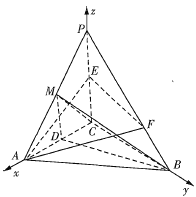
【題目】如圖,在三棱錐PABC中,![]() 底面ABC,
底面ABC,![]() ,
,![]() ,
,![]() ,D,E分別是AC,PC的中點(diǎn),F是PB上一點(diǎn),且
,D,E分別是AC,PC的中點(diǎn),F是PB上一點(diǎn),且![]() ,M為PA的中點(diǎn),二面角
,M為PA的中點(diǎn),二面角![]() 的大小為45°.
的大小為45°.

(1)證明:![]() 平面AEF;
平面AEF;
(2)求直線(xiàn)AF與平面BCM所成角的正弦值.
【答案】(1)證明見(jiàn)解析;(2)![]()
【解析】
(1)連接PD交AE于點(diǎn)O,因?yàn)?/span>D,E分別是AC,PC的中點(diǎn),則點(diǎn)O是![]() 的重心,所以
的重心,所以![]() ,連接OF,又
,連接OF,又![]() ,所以
,所以![]() ,從而可證明結(jié)論.
,從而可證明結(jié)論.
(2)由題意可證得![]() 即二面角
即二面角![]() 的平面角,即
的平面角,即![]() ,可得
,可得![]() ,則
,則![]() ,得到
,得到![]() ,又由題意易知,CA,CB,CP兩兩垂直,故以C為坐標(biāo)原點(diǎn),直線(xiàn)CA,CB,CP所在直線(xiàn)分別為x軸、y軸、z軸建立如圖所示的空間直角坐標(biāo)系
,又由題意易知,CA,CB,CP兩兩垂直,故以C為坐標(biāo)原點(diǎn),直線(xiàn)CA,CB,CP所在直線(xiàn)分別為x軸、y軸、z軸建立如圖所示的空間直角坐標(biāo)系![]() ,用向量法求解線(xiàn)面角.
,用向量法求解線(xiàn)面角.
解:(1)連接PD交AE于點(diǎn)O,因?yàn)?/span>D,E分別是AC,PC的中點(diǎn),
所以點(diǎn)O是![]() 的重心,所以
的重心,所以![]() .
.
連接OF,又![]() ,所以
,所以![]() ,則
,則![]() .
.
又![]() 平面AEF,
平面AEF,![]() 平面AEF,所以
平面AEF,所以![]() 平面AEF.
平面AEF.
(2)因?yàn)?/span>![]() 底面ABC,
底面ABC,![]() 平面ABC,所以
平面ABC,所以![]() .又
.又![]() ,
,![]() ,
,
所以![]() 平面PAC.所以
平面PAC.所以![]() ,又
,又![]() ,所以
,所以![]() 即二面角
即二面角![]() 的平面角,
的平面角,
所以![]() ,連接MD,易得
,連接MD,易得![]() ,則
,則![]() ,所以
,所以![]() .
.
由題意易知,CA,CB,CP兩兩垂直,故以C為坐標(biāo)原點(diǎn),直線(xiàn)CA,CB,CP所在直線(xiàn)分別為x軸、y軸、z軸建立如圖所示的空間直角坐標(biāo)系![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,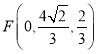 ,
,
所以![]() ,
,![]() ,
,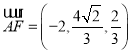 .
.
設(shè)平面BCM的法向量為![]() ,則
,則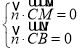 ,得
,得 ,得
,得![]() ,
,
令![]() ,則
,則![]() ,所以
,所以![]() 為平面BCM的一個(gè)法向量.
為平面BCM的一個(gè)法向量.
設(shè)直線(xiàn)AF與平面BCM所成的角為![]() .
.
則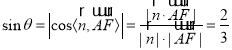
故直線(xiàn)AF與平面BCM所成角的正弦值為![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若函數(shù)![]() 在
在![]() 處取得極大值或極小值,則稱(chēng)
處取得極大值或極小值,則稱(chēng)![]() 為函數(shù)
為函數(shù)![]() 的極值點(diǎn).設(shè)函數(shù)
的極值點(diǎn).設(shè)函數(shù)![]() .
.
(1)若函數(shù)![]() 在
在![]() 上無(wú)極值點(diǎn),求
上無(wú)極值點(diǎn),求![]() 的取值范圍;
的取值范圍;
(2)求證:對(duì)任意實(shí)數(shù)![]() ,在函數(shù)
,在函數(shù)![]() 的圖象上總存在兩條切線(xiàn)相互平行;
的圖象上總存在兩條切線(xiàn)相互平行;
(3)當(dāng)![]() 時(shí),若函數(shù)
時(shí),若函數(shù)![]() 的圖象上存在的兩條平行切線(xiàn)之間的距離為4,問(wèn);這樣的平行切線(xiàn)共有幾組?請(qǐng)說(shuō)明理由.
的圖象上存在的兩條平行切線(xiàn)之間的距離為4,問(wèn);這樣的平行切線(xiàn)共有幾組?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
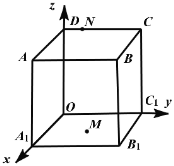
【題目】單位正方體![]() 在空間直角坐標(biāo)系中的位置如圖所示,動(dòng)點(diǎn)
在空間直角坐標(biāo)系中的位置如圖所示,動(dòng)點(diǎn)![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,設(shè)由
,設(shè)由![]() ,
,![]() ,
,![]() 三點(diǎn)確定的平面截該正方體的截面為
三點(diǎn)確定的平面截該正方體的截面為![]() ,那么( )
,那么( )
A.對(duì)任意點(diǎn)![]() ,存在點(diǎn)
,存在點(diǎn)![]() 使截面
使截面![]() 為三角形
為三角形
B.對(duì)任意點(diǎn)![]() ,存在點(diǎn)
,存在點(diǎn)![]() 使截面
使截面![]() 為正方形
為正方形
C.對(duì)任意點(diǎn)![]() 和
和![]() ,截面
,截面![]() 都為梯形
都為梯形
D.對(duì)任意點(diǎn)![]() ,存在點(diǎn)
,存在點(diǎn)![]() 使得截面
使得截面![]() 為矩形
為矩形
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校![]() 名學(xué)生參加軍事冬令營(yíng)活動(dòng),活動(dòng)期間各自扮演一名角色進(jìn)行分組游戲,角色按級(jí)別從小到大共
名學(xué)生參加軍事冬令營(yíng)活動(dòng),活動(dòng)期間各自扮演一名角色進(jìn)行分組游戲,角色按級(jí)別從小到大共![]() 種,分別為士兵、排長(zhǎng)、連長(zhǎng)、營(yíng)長(zhǎng)、團(tuán)長(zhǎng)、旅長(zhǎng)、師長(zhǎng)、軍長(zhǎng)和司令.游戲分組有兩種方式,可以
種,分別為士兵、排長(zhǎng)、連長(zhǎng)、營(yíng)長(zhǎng)、團(tuán)長(zhǎng)、旅長(zhǎng)、師長(zhǎng)、軍長(zhǎng)和司令.游戲分組有兩種方式,可以![]() 人一組或者
人一組或者![]() 人一組.如果
人一組.如果![]() 人一組,則必須角色相同;如果
人一組,則必須角色相同;如果![]() 人一組,則
人一組,則![]() 人角色相同或者
人角色相同或者![]() 人為級(jí)別連續(xù)的
人為級(jí)別連續(xù)的![]() 個(gè)不同角色.已知這
個(gè)不同角色.已知這![]() 名學(xué)生扮演的角色有
名學(xué)生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,現(xiàn)在新加入
人,現(xiàn)在新加入![]() 名學(xué)生,將這
名學(xué)生,將這![]() 名學(xué)生分成
名學(xué)生分成![]() 組進(jìn)行游戲,則新加入的學(xué)生可以扮演的角色的種數(shù)為________.
組進(jìn)行游戲,則新加入的學(xué)生可以扮演的角色的種數(shù)為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() .
.
(1)當(dāng)![]() 時(shí),證明:函數(shù)
時(shí),證明:函數(shù)![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
(2)若![]() ,討論函數(shù)
,討論函數(shù)![]() 零點(diǎn)的個(gè)數(shù).
零點(diǎn)的個(gè)數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市數(shù)學(xué)教研室對(duì)全市2018級(jí)15000名的高中生的學(xué)業(yè)水平考試的數(shù)學(xué)成績(jī)進(jìn)行調(diào)研,隨機(jī)選取了200名高中生的學(xué)業(yè)水平考試的數(shù)學(xué)成績(jī)作為樣本進(jìn)行分析,將結(jié)果列成頻率分布表如下:
數(shù)學(xué)成績(jī) | 頻數(shù) | 頻率 |
| 5 | 0.025 |
| 15 | 0.075 |
| 50 | 0.25 |
| 70 | 0.35 |
| 45 | 0.225 |
| 15 | 0.075 |
合計(jì) | 200 | 1 |
根據(jù)學(xué)業(yè)水平考試的數(shù)學(xué)成績(jī)將成績(jī)分為“優(yōu)秀”、“合格”、“不合格”三個(gè)等級(jí),其中成績(jī)大于或等于80分的為“優(yōu)秀”,成績(jī)小于60分的為“不合格”,其余的成績(jī)?yōu)椤昂细瘛?/span>.
(1)根據(jù)頻率分布表中的數(shù)據(jù),估計(jì)全市學(xué)業(yè)水平考試的數(shù)學(xué)成績(jī)的眾數(shù)、中位數(shù)(精確到0.1);
(2)市數(shù)學(xué)教研員從樣本中又隨機(jī)選取了![]() 名高中生的學(xué)業(yè)水平考試的數(shù)學(xué)成績(jī),如果這
名高中生的學(xué)業(yè)水平考試的數(shù)學(xué)成績(jī),如果這![]() 的最小值;
的最小值;
(3)估計(jì)全市2018級(jí)高中生學(xué)業(yè)水平考試“不合格”的人數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某工廠質(zhì)檢部門(mén)要對(duì)該廠流水線(xiàn)生產(chǎn)出的一批產(chǎn)品進(jìn)行檢驗(yàn),如果檢查到第![]() 件仍未發(fā)現(xiàn)不合格品,則此次檢查通過(guò)且認(rèn)為這批產(chǎn)品合格,如果在尚未抽到第
件仍未發(fā)現(xiàn)不合格品,則此次檢查通過(guò)且認(rèn)為這批產(chǎn)品合格,如果在尚未抽到第![]() 件時(shí)已檢查到不合格品則拒絕通過(guò)且認(rèn)為這批產(chǎn)品不合格.設(shè)這批產(chǎn)品的數(shù)量足夠大,可以認(rèn)為每次檢查查到不合格品的概率都為
件時(shí)已檢查到不合格品則拒絕通過(guò)且認(rèn)為這批產(chǎn)品不合格.設(shè)這批產(chǎn)品的數(shù)量足夠大,可以認(rèn)為每次檢查查到不合格品的概率都為![]() ,即每次抽查的產(chǎn)品是相互獨(dú)立的.
,即每次抽查的產(chǎn)品是相互獨(dú)立的.
(1)若![]() ,求這批產(chǎn)品能夠通過(guò)檢查的概率;
,求這批產(chǎn)品能夠通過(guò)檢查的概率;
(2)已知每件產(chǎn)品質(zhì)檢費(fèi)用為50元,若![]() ,設(shè)對(duì)這批產(chǎn)品的質(zhì)檢個(gè)數(shù)記作
,設(shè)對(duì)這批產(chǎn)品的質(zhì)檢個(gè)數(shù)記作![]() ,求
,求![]() 的分布列;
的分布列;
(3)在(2)的條件下,已知1000批此類(lèi)產(chǎn)品,若![]() ,則總平均檢查費(fèi)用至少需要多少元?(總平均檢查費(fèi)用
,則總平均檢查費(fèi)用至少需要多少元?(總平均檢查費(fèi)用![]() 每批次平均檢查費(fèi)用
每批次平均檢查費(fèi)用![]() 批數(shù))
批數(shù))
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖![]() ,某十字路口的花圃中央有一個(gè)底面半徑為
,某十字路口的花圃中央有一個(gè)底面半徑為![]() 的圓柱形花柱,四周斑馬線(xiàn)的內(nèi)側(cè)連線(xiàn)構(gòu)成邊長(zhǎng)為
的圓柱形花柱,四周斑馬線(xiàn)的內(nèi)側(cè)連線(xiàn)構(gòu)成邊長(zhǎng)為![]() 的正方形.因工程需要,測(cè)量員將使用儀器沿斑馬線(xiàn)的內(nèi)側(cè)進(jìn)行測(cè)量,其中儀器
的正方形.因工程需要,測(cè)量員將使用儀器沿斑馬線(xiàn)的內(nèi)側(cè)進(jìn)行測(cè)量,其中儀器![]() 的移動(dòng)速度為
的移動(dòng)速度為![]() ,儀器
,儀器![]() 的移動(dòng)速度為
的移動(dòng)速度為![]() .若儀器
.若儀器![]() 與儀器
與儀器![]() 的對(duì)視光線(xiàn)被花柱阻擋,則稱(chēng)儀器
的對(duì)視光線(xiàn)被花柱阻擋,則稱(chēng)儀器![]() 在儀器
在儀器![]() 的“盲區(qū)”中.
的“盲區(qū)”中.



(1)如圖![]() ,斑馬線(xiàn)的內(nèi)側(cè)連線(xiàn)構(gòu)成正方形
,斑馬線(xiàn)的內(nèi)側(cè)連線(xiàn)構(gòu)成正方形![]() ,儀器
,儀器![]() 在點(diǎn)
在點(diǎn)![]() 處,儀器
處,儀器![]() 在
在![]() 上距離點(diǎn)
上距離點(diǎn)![]()
![]() 處,試判斷儀器
處,試判斷儀器![]() 是否在儀器
是否在儀器![]() 的“盲區(qū)”中,并說(shuō)明理由;
的“盲區(qū)”中,并說(shuō)明理由;
(2)如圖![]() ,斑馬線(xiàn)的內(nèi)側(cè)連線(xiàn)構(gòu)成正方形
,斑馬線(xiàn)的內(nèi)側(cè)連線(xiàn)構(gòu)成正方形![]() ,儀器
,儀器![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)向點(diǎn)
出發(fā)向點(diǎn)![]() 移動(dòng),同時(shí)儀器
移動(dòng),同時(shí)儀器![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)向點(diǎn)
出發(fā)向點(diǎn)![]() 移動(dòng),在這個(gè)移動(dòng)過(guò)程中,儀器
移動(dòng),在這個(gè)移動(dòng)過(guò)程中,儀器![]() 在儀器
在儀器![]() 的“盲區(qū)”中的時(shí)長(zhǎng)為多少?
的“盲區(qū)”中的時(shí)長(zhǎng)為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方形![]() 、
、![]() 的邊長(zhǎng)都是1,而且平面
的邊長(zhǎng)都是1,而且平面![]() 、
、![]() 互相垂直.點(diǎn)M在
互相垂直.點(diǎn)M在![]() 上移動(dòng),點(diǎn)N在
上移動(dòng),點(diǎn)N在![]() 上移動(dòng),若
上移動(dòng),若![]() (
(![]() ).
).

(1)當(dāng)a為何值時(shí),![]() 的長(zhǎng)最小;
的長(zhǎng)最小;
(2)當(dāng)![]() 長(zhǎng)最小時(shí),求面
長(zhǎng)最小時(shí),求面![]() 與面
與面![]() 所成的二面角α的余弦值.
所成的二面角α的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com