
【題目】在底面是邊長為6的正方形的四棱錐P--ABCD中,點P在底面的射影H為正方形ABCD的中心,異面直線PB與AD所成角的正切值為![]() ,則四棱錐P--ABCD的內切球與外接球的半徑之比為( )
,則四棱錐P--ABCD的內切球與外接球的半徑之比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
確定異面直線PB與AD所成角為∠PBC,取BC中點E,則tan∠PBC![]() ,求出PE=5,HP=4,可得四棱錐P﹣ABCD的表面積、體積,進而求出內切球的半徑,利用勾股定理求出外接球的半徑,即可求出四棱錐P﹣ABCD的內切球與外接球的半徑之比.
,求出PE=5,HP=4,可得四棱錐P﹣ABCD的表面積、體積,進而求出內切球的半徑,利用勾股定理求出外接球的半徑,即可求出四棱錐P﹣ABCD的內切球與外接球的半徑之比.
由題意,四棱錐P﹣ABCD為正四棱錐,PA=PB=PC=PD,
∵AD∥BC,
∴異面直線PB與AD所成角為∠PBC,
取BC中點E,則tan∠PBC![]() ,
,
∴PE=5,HP=4,
從而四棱錐P﹣ABCD的表面積為S![]() 96,V
96,V![]() 48,
48,
∴內切球的半徑為r![]() .
.
設四棱錐P﹣ABCD外接球的球心為O,外接球的半徑為R,則OP=OA,
∴(4﹣R)2+(3![]() )2=R2,
)2=R2,
∴R![]() ,
,
∴![]() .
.
故選D.


科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC—A1B1C1中,側棱與底面垂直,∠BAC=90°,AB=AC=AA1=2,點M,N分別為A1B和B1C1的中點.
(1)求異面直線A1B與NC所成角的余弦值;
(2)求A1B與平面NMC所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】邊長為2的正三角形ABC中,點D,E,G分別是邊AB,AC,BC的中點,連接DE,連接AG交DE于點![]() 現將
現將![]() 沿DE折疊至
沿DE折疊至![]() 的位置,使得平面
的位置,使得平面![]() 平面BCED,連接A1G,EG.
平面BCED,連接A1G,EG.
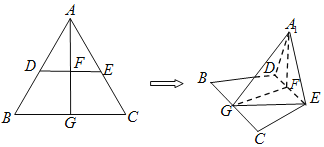
![]() 證明:DE∥平面A1BC
證明:DE∥平面A1BC
![]() 求點B到平面A1EG的距離.
求點B到平面A1EG的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 是定義在
是定義在![]() 上的偶函數,當
上的偶函數,當![]() 時,
時, ![]() ).
).
(1)當![]() 時,求
時,求![]() 的解析式;
的解析式;
(2)若![]() ,試判斷
,試判斷![]() 的上單調性,并證明你的結論;
的上單調性,并證明你的結論;
(3)是否存在![]() ,使得當
,使得當![]() 時,
時, ![]() 有最大值
有最大值![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com