
【題目】設等差數列{an}的公差為d,前n項和為Sn , 等比數列{bn}的公比為q,已知b1=a1 , b2=2,q=d,S10=100.
(1)求數列{an},{bn}的通項公式
(2)當d>1時,記cn= ![]() ,求數列{cn}的前n項和Tn .
,求數列{cn}的前n項和Tn .
【答案】
(1)解:設a1=a,由題意可得 ![]() ,
,
解得 ![]() ,或
,或 ![]() ,
,
當 ![]() 時,an=2n﹣1,bn=2n﹣1;
時,an=2n﹣1,bn=2n﹣1;
當 ![]() 時,an=
時,an= ![]() (2n+79),bn=9
(2n+79),bn=9 ![]()
(2)解:當d>1時,由(1)知an=2n﹣1,bn=2n﹣1,
∴cn= ![]() =
= ![]() ,
,
∴Tn=1+3 ![]() +5
+5 ![]() +7
+7 ![]() +9
+9 ![]() +…+(2n﹣1)
+…+(2n﹣1) ![]() ,
,
∴ ![]() Tn=1
Tn=1 ![]() +3
+3 ![]() +5
+5 ![]() +7
+7 ![]() +…+(2n﹣3)
+…+(2n﹣3) ![]() +(2n﹣1)
+(2n﹣1) ![]() ,
,
∴ ![]() Tn=2+
Tn=2+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣(2n﹣1)
﹣(2n﹣1) ![]() =3﹣
=3﹣ ![]() ,
,
∴Tn=6﹣ ![]()
【解析】(1)利用前10項和與首項、公差的關系,聯立方程組計算即可;(2)當d>1時,由(1)知cn= ![]() ,寫出Tn、
,寫出Tn、 ![]() Tn的表達式,利用錯位相減法及等比數列的求和公式,計算即可.
Tn的表達式,利用錯位相減法及等比數列的求和公式,計算即可.
【考點精析】解答此題的關鍵在于理解數列的前n項和的相關知識,掌握數列{an}的前n項和sn與通項an的關系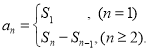 .
.


科目:高中數學 來源: 題型:
【題目】某車間為了規定工時定額,需要確定加工零件所花費的時間,為此進行了5次試驗,收集數據如下表:
加工零件個數x/個 | 10 | 20 | 30 | 40 | 50 |
加工時間y/分鐘 | 64 | 69 | 75 | 82 | 90 |
經檢驗,這組樣本數據具有線性相關關系,那么對于加工零件的個數x與加工時間y這兩個變量,下列判斷正確的是( )
A. 成正相關,其回歸直線經過點(30,75)
B. 成正相關,其回歸直線經過點(30,76)
C. 成負相關,其回歸直線經過點(30,76)
D. 成負相關,其回歸直線經過點(30,75)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若a,b是函數f(x)=x2﹣px+q(p>0,q>0)的兩個不同的零點,且a,b,﹣2這三個數可適當排序后成等差數列,也可適當排序后成等比數列,則p+q的值等于( )
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知條件p:A={x|x2﹣2mx+m2﹣4≤0,x∈R,m∈R},條件q:B={x|x2﹣2x﹣3≤0,x∈R}.
(1)若A∩B={x|0≤x≤3},求實數m的值;
(2)若q是¬p的充分條件,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從橢圓![]() 上一點
上一點![]() 向
向![]() 軸作垂線,垂足恰好為橢圓的左焦點
軸作垂線,垂足恰好為橢圓的左焦點![]() ,
, ![]() 是橢圓的右頂點,
是橢圓的右頂點, ![]() 是橢圓的上頂點,且
是橢圓的上頂點,且![]() .
.
(1)求該橢圓![]() 的方程;
的方程;
(2)不過原點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,已知
兩點,已知![]() ,直線
,直線![]() ,
, ![]() 的斜率
的斜率![]() ,
, ![]() 成等比數列,記以
成等比數列,記以![]() ,
, ![]() 為直徑的圓的面積分別為
為直徑的圓的面積分別為![]() ,求證;
,求證; ![]() 為定值,并求出定值.
為定值,并求出定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率
,離心率![]() ,
, ![]() 為橢圓
為橢圓![]() 上的任意一點(不含長軸端點),且
上的任意一點(不含長軸端點),且![]() 面積的最大值為1.
面積的最大值為1.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,且線段
,且線段![]() 的中點不在圓
的中點不在圓![]() 內,求
內,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國人均讀書4.3本(包括網絡文學和教科書),比韓國的11本、法國的20本、日本的40本、猶太人的64本少得多,是世界上人均讀書最少的國家.”這個論斷被各種媒體反復引用.出現這樣的統計結果無疑是令人尷尬的,而且和其他國家相比,我國國民的閱讀量如此之低,也和我國是傳統的文明古國、禮儀之邦的地位不相符.某小區為了提高小區內人員的讀書興趣,特舉辦讀書活動,準備進一定量的書籍豐富小區圖書站,由于不同年齡段需看不同類型的書籍,為了合理配備資源,現對小區內看書人員進行年齡調查,隨機抽取了一天 ![]() 名讀書者進行調查,將他們的年齡分成6段:
名讀書者進行調查,將他們的年齡分成6段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如圖所示的頻率分布直方圖.問:
后得到如圖所示的頻率分布直方圖.問:
(1)估計在40名讀書者中年齡分布在 ![]() 的人數;
的人數;
(2)求40名讀書者年齡的平均數和中位數;
(3)若從年齡在 ![]() 的讀書者中任取2名,求這兩名讀書者年齡在
的讀書者中任取2名,求這兩名讀書者年齡在 ![]() 的人數
的人數 ![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com