
【題目】某公司為了提高利潤,從2012年至2018年每年對生產環節的改進進行投資,投資金額與年利潤增長的數據如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投資金額 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利潤增長 | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
(1)請用最小二乘法求出![]() 關于
關于![]() 的回歸直線方程(結果保留兩位小數);
的回歸直線方程(結果保留兩位小數);
(2)現從2012—2018年這7年中抽出三年進行調查,記![]() 年利潤增長-投資金額,設這三年中
年利潤增長-投資金額,設這三年中![]() (萬元)的年份數為
(萬元)的年份數為![]() ,求隨機變量
,求隨機變量![]() 的分布列與期望.
的分布列與期望.
參考公式: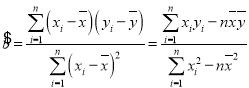 ,
,![]() .
.
參考數據:![]() ,
,![]() .
.
 核心素養學練評系列答案
核心素養學練評系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,以坐標原點為極點,以![]() 軸正半軸為極軸,建立極坐標系,點
軸正半軸為極軸,建立極坐標系,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() ,且
,且![]() 過點
過點![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為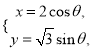 (
(![]() 為參數).
為參數).
(Ⅰ)求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值;
的距離的最大值;
(Ⅱ)過點![]() 與直線
與直線![]() 平行的直線
平行的直線![]() 與曲線
與曲線 ![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代儒家要求學生掌握六種基本才藝:禮、樂、射、御、書、數,簡稱“六藝”,某高中學校為弘揚“六藝”的傳統文化,分別進行了主題為“禮、樂、射、御、書、數”六場傳統文化知識競賽,現有甲、乙、丙三位選手進入了前三名的最后角逐,規定:每場知識競賽前三名的得分都分別為![]()
![]() 且
且![]() ;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為
;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
A. 乙有四場比賽獲得第三名
B. 每場比賽第一名得分![]() 為
為![]()
C. 甲可能有一場比賽獲得第二名
D. 丙可能有一場比賽獲得第一名
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某區“創文明城區”(簡稱“創城”)活動中,教委對本區![]() 四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
學校 |
|
|
|
|
抽查人數 | 50 | 15 | 10 | 25 |
“創城”活動中參與的人數 | 40 | 10 | 9 | 15 |
(注:參與率是指:一所學校“創城”活動中參與的人數與被抽查人數的比值)假設每名高中學生是否參與”創城”活動是相互獨立的.
(1)若該區共2000名高中學生,估計![]() 學校參與“創城”活動的人數;
學校參與“創城”活動的人數;
(2)在隨機抽查的100名高中學生中,隨機抽取1名學生,求恰好該生沒有參與“創城”活動的概率;
(3)在上表中從![]() 兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好
兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好![]() 兩校各有1人沒有參與“創城”活動的概率是多少?
兩校各有1人沒有參與“創城”活動的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩支籃球隊賽季總決賽采用7場4勝制,每場必須分出勝負,場與場之間互不影響,只要有一隊獲勝4場就結束比賽.現已比賽了4場,且甲籃球隊勝3場.已知甲球隊第5,6場獲勝的概率均為![]() ,但由于體力原因,第7場獲勝的概率為
,但由于體力原因,第7場獲勝的概率為![]() .
.
(1)求甲隊分別以![]() ,
,![]() 獲勝的概率;
獲勝的概率;
(2)設![]() 表示決出冠軍時比賽的場數,求
表示決出冠軍時比賽的場數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的離心率為
的離心率為![]() ,過橢圓右焦點
,過橢圓右焦點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() 與
與![]() .當直線
.當直線![]() 的斜率為0時,
的斜率為0時,![]() .
.
(1)求橢圓的方程;
(2)試探究![]() 是否為定值?若是,證明你的結論;若不是,請說明理由.
是否為定值?若是,證明你的結論;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一個半徑為2千米,圓心角為![]() 的扇形游覽區的平面示意圖
的扇形游覽區的平面示意圖![]() 是半徑
是半徑![]() 上一點,
上一點,![]() 是圓弧
是圓弧![]() 上一點,且
上一點,且![]() .現在線段
.現在線段![]() ,線段
,線段![]() 及圓弧
及圓弧![]() 三段所示位置設立廣告位,經測算廣告位出租收入是:線段
三段所示位置設立廣告位,經測算廣告位出租收入是:線段![]() 處每千米為
處每千米為![]() 元,線段
元,線段![]() 及圓弧
及圓弧![]() 處每千米均為
處每千米均為![]() 元.設
元.設![]() 弧度,廣告位出租的總收入為
弧度,廣告位出租的總收入為![]() 元.
元.
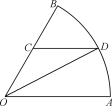
(1)求![]() 關于
關于![]() 的函數解析式,并指出該函數的定義域;
的函數解析式,并指出該函數的定義域;
(2)試問:![]() 為何值時,廣告位出租的總收入最大?并求出其最大值.
為何值時,廣告位出租的總收入最大?并求出其最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com