
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)當(dāng)![]() ,
,![]() 時,求函數(shù)
時,求函數(shù)![]() 在
在![]() 處的切線方程,并求函數(shù)
處的切線方程,并求函數(shù)![]() 的最大值;
的最大值;
(2)若函數(shù)![]() 的兩個零點分別為
的兩個零點分別為![]() ,
,![]() ,且
,且![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】
(1)當(dāng)![]() 時,求得斜率和切點的坐標(biāo),利用點斜式寫出切線方程.根據(jù)函數(shù)的導(dǎo)數(shù)求得函數(shù)的單調(diào)區(qū)間,由此求得函數(shù)的最大值.(2)將兩個零點代入函數(shù)
時,求得斜率和切點的坐標(biāo),利用點斜式寫出切線方程.根據(jù)函數(shù)的導(dǎo)數(shù)求得函數(shù)的單調(diào)區(qū)間,由此求得函數(shù)的最大值.(2)將兩個零點代入函數(shù)![]() 的解析式,將得到兩個方程相減,化簡為
的解析式,將得到兩個方程相減,化簡為![]() 的表達(dá)式,通過令
的表達(dá)式,通過令![]() ,將所要證明的不等式轉(zhuǎn)化為證明
,將所要證明的不等式轉(zhuǎn)化為證明![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,利用導(dǎo)數(shù)證明
,利用導(dǎo)數(shù)證明![]() ,由此證得原不等式成立.
,由此證得原不等式成立.
(1)解:當(dāng)![]() ,
,![]() 時,
時,![]() ,
,![]() ,
,
則![]() ,切點為
,切點為![]() ,故函數(shù)
,故函數(shù)![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
令![]() ,則
,則![]() 在
在![]() 是減函數(shù),
是減函數(shù),
又![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 在
在![]() 上是增函數(shù),在
上是增函數(shù),在![]() 是減函數(shù),
是減函數(shù),![]() .
.
(2)證明:∵![]() ,
,![]() 是
是![]() 的兩個零點,不妨設(shè)
的兩個零點,不妨設(shè)![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
相減得:![]()
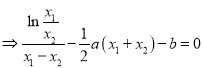
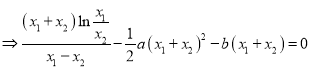 ,
,
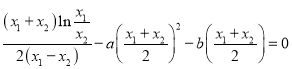 ,
,
∴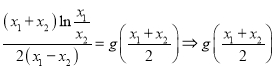
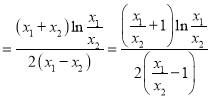 ,
,
令![]() ,即證
,即證![]() ,
,![]() ,
,
![]() ,
,
令![]() ,
,![]() ,
,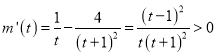 ,
,
![]() 在
在![]() 上是增函數(shù),又∵
上是增函數(shù),又∵![]() ,
,
∴![]() ,
,![]() ,命題得證.
,命題得證.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】華為董事會決定投資開發(fā)新款軟件,估計能獲得![]() 萬元到
萬元到![]() 萬元的投資收益,討論了一個對課題組的獎勵方案:獎金
萬元的投資收益,討論了一個對課題組的獎勵方案:獎金![]() (單位:萬元)隨投資收益
(單位:萬元)隨投資收益![]() (單位:萬元)的增加而增加,且獎金不超過
(單位:萬元)的增加而增加,且獎金不超過![]() 萬元,同時獎金不超過投資收益的
萬元,同時獎金不超過投資收益的![]() .
.
(1)請分析函數(shù)![]() 是否符合華為要求的獎勵函數(shù)模型,并說明原因;
是否符合華為要求的獎勵函數(shù)模型,并說明原因;
(2)若華為公司采用模型函數(shù)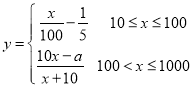 作為獎勵函數(shù)模型,試確定正整數(shù)
作為獎勵函數(shù)模型,試確定正整數(shù)![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為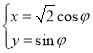 (
(![]() 為參數(shù)),以坐標(biāo)原點
為參數(shù)),以坐標(biāo)原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的極坐標(biāo)方程和
的極坐標(biāo)方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)![]() 是曲線
是曲線![]() 上一點,此時參數(shù)
上一點,此時參數(shù)![]() ,將射線
,將射線![]() 繞原點
繞原點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 交曲線
交曲線![]() 于點
于點![]() ,記曲線
,記曲線![]() 的上頂點為點
的上頂點為點![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列![]() 的前n項和
的前n項和![]() ,且滿足
,且滿足![]() ,
,![]() ,數(shù)列
,數(shù)列![]() 是首項為2,公比為q(
是首項為2,公比為q(![]() )的等比數(shù)列.
)的等比數(shù)列.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設(shè)正整數(shù)k,t,r成等差數(shù)列,且![]() ,若
,若![]() ,求實數(shù)q的最大值;
,求實數(shù)q的最大值;
(3)若數(shù)列![]() 滿足
滿足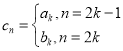 ,
,![]() ,其前n項和為
,其前n項和為![]() ,當(dāng)
,當(dāng)![]() 時,是否存在正整數(shù)m,使得
時,是否存在正整數(shù)m,使得![]() 恰好是數(shù)列
恰好是數(shù)列![]() 中的項?若存在,求岀m的值;若不存在,說明理由.
中的項?若存在,求岀m的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若二次函數(shù)g(x)=ax2+bx+c(a≠0)滿足g(x+1)=2x+g(x),且g(0)=1.
(1)求g(x)的解析式;
(2)若在區(qū)間[-1,1]上,不等式g(x)-t>2x恒成立,求實數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)統(tǒng)計,某蔬菜基地西紅柿畝產(chǎn)量的增加量![]() (百千克)與某種液體肥料每畝使用量
(百千克)與某種液體肥料每畝使用量![]() (千克)之間的對應(yīng)數(shù)據(jù)的散點圖,如圖所示.
(千克)之間的對應(yīng)數(shù)據(jù)的散點圖,如圖所示.

(1)依據(jù)數(shù)據(jù)的散點圖可以看出,可用線性回歸模型擬合![]() 與
與![]() 的關(guān)系,請計算相關(guān)系數(shù)
的關(guān)系,請計算相關(guān)系數(shù)![]() 并加以說明(若
并加以說明(若![]() ,則線性相關(guān)程度很高,可用線性回歸模型擬合);
,則線性相關(guān)程度很高,可用線性回歸模型擬合);
(2)求![]() 關(guān)于
關(guān)于![]() 的回歸方程,并預(yù)測液體肥料每畝使用量為12千克時,西紅柿畝產(chǎn)量的增加量
的回歸方程,并預(yù)測液體肥料每畝使用量為12千克時,西紅柿畝產(chǎn)量的增加量![]() 約為多少?
約為多少?
附:相關(guān)系數(shù)公式
 ,參考數(shù)據(jù):
,參考數(shù)據(jù):![]() ,
,![]() .
.
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論![]() 的單調(diào)性并指出相應(yīng)單調(diào)區(qū)間;
的單調(diào)性并指出相應(yīng)單調(diào)區(qū)間;
(2)若![]() ,設(shè)
,設(shè)![]() 是函數(shù)
是函數(shù)![]() 的兩個極值點,若
的兩個極值點,若![]() ,且
,且![]() 恒成立,求實數(shù)k的取值范圍.
恒成立,求實數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 有兩個零點
有兩個零點![]() ,
,![]() (
(![]() ).
).
(i)求![]() 的取值范圍;
的取值范圍;
(ii)求證:![]() 隨著
隨著![]() 的增大而增大.
的增大而增大.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com