
(本小題滿分14分)
已知二次函數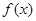 滿足以下兩個條件:
滿足以下兩個條件:
①不等式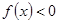 的解集是(-2,0) ②函數
的解集是(-2,0) ②函數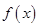 在
在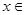
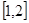 上的最小值是3
上的最小值是3
(Ⅰ)求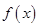 的解析式;
的解析式;
(Ⅱ)若點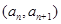
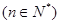 在函數
在函數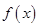 的圖象上,且
的圖象上,且
(ⅰ)求證:數列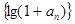 為等比數列
為等比數列
(ⅱ)令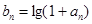 ,是否存在正實數
,是否存在正實數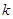 ,使不等式
,使不等式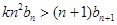 對于一切的
對于一切的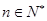 恒成立?若存在,指出
恒成立?若存在,指出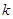 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
(Ⅰ)f(x)=" x" 2 + 2 x .
(Ⅱ)(ⅰ)見解析;(ⅱ)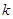
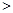

解析試題分析:(Ⅰ)因為根據題意可知f(x)< 0 的解集為(-2,0),且f(x)是二次函數
因此可設 f(x)=" a" x(x + 2) (a > 0),故 f(x)的對稱軸為直線 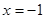 ,
,
f(x)在 [1,2]上的最小值為f(1)="3a" ="3" ,得到參數a的值。
(Ⅱ)(ⅰ)因為點(a n , a n + 1 )在函數f(x)=" x" 2 + 2 x 的圖象上
∴得到遞推關系式 a n + 1 =" a" n 2 + 2 a n , 構造等比數列求解通項公式。
(ⅱ)由上題可知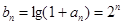 ,要使得不等式
,要使得不等式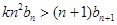 恒成立,即
恒成立,即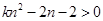 對于一切的
對于一切的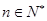 恒成立,轉換為二次不等式求解。
恒成立,轉換為二次不等式求解。
解:(Ⅰ)∵ f(x)< 0 的解集為(-2,0),且f(x)是二次函數
∴ 可設 f(x)=" a" x(x + 2) (a > 0),故 f(x)的對稱軸為直線 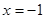 ,
,
∴ f(x)在 [1,2]上的最小值為f(1)="3a" ="3" ,
∴ a =" 1" ,所以f(x)=" x" 2 + 2 x .
(Ⅱ)(ⅰ)∵ 點(a n , a n + 1 )在函數f(x)=" x" 2 + 2 x 的圖象上,
∴ a n + 1 =" a" n 2 + 2 a n ,則 1 + a n + 1 =" 1" + a n 2 + 2 a n = (1 + a n)2
∴ 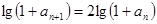 , 又首項
, 又首項 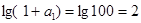
∴ 數列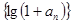 為等比數列,且公比為2 。
為等比數列,且公比為2 。
(ⅱ)由上題可知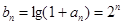 ,要使得不等式
,要使得不等式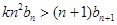 恒成立,即
恒成立,即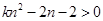 對于一切的
對于一切的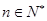 恒成立,
恒成立,
法一: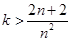 對一切的
對一切的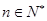 恒成立,
恒成立,
令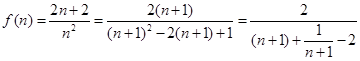 ,
,
∵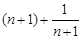 在
在 是單調遞增的,∴
是單調遞增的,∴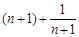 的最小值為
的最小值為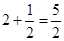
 =
=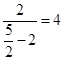 所以
所以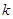

法二:
設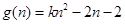
當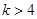 時,由于對稱軸直線
時,由于對稱軸直線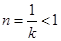 ,且
,且 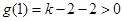 ,而函數
,而函數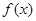 在
在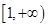 是增函數,∴不等式
是增函數,∴不等式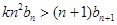 恒成立
恒成立
即當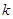
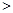
 時,不等式
時,不等式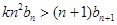 對于一切的
對于一切的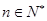 恒成立
恒成立
考點:本試題主要考查了數列、不等式知識,考查化歸與轉化、分類與整合的數學思想,培養學生的抽象概括能力、推理論證能力、運算求解能力和創新意識.
點評:解題時要注意對于不等式恒成立問題的等價轉化為一元二次不等式問題。


 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:高中數學 來源: 題型:解答題
(12分)已知函數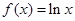 ,
, ,設
,設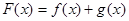 .
.
(1)求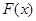 的單調區間;
的單調區間;
(2)若以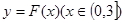 圖象上任意一點
圖象上任意一點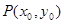 為切點的切線的斜率
為切點的切線的斜率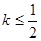
恒成立,求實數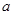 的最小值.
的最小值.
(3)是否存在實數 ,使得函數
,使得函數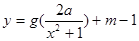 的圖象與
的圖象與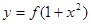 的圖
的圖
象恰好有四個不同的交點?若存在,求出 的取值范圍,若不存在,說明理由.
的取值范圍,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(10分)已知函數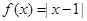
(1)用分段函數的形式表示該函數;
(2)在坐標系中畫出該函數的圖像
(3)寫出該函數的定義域,值域,奇偶性和單調區間(不要求證明)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com