
【題目】已知數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)設數列![]() 滿足
滿足 ,其中
,其中![]() .記
.記![]() 的前
的前![]() 項和為
項和為![]() .是否存在正整數
.是否存在正整數![]()
![]() ,使得
,使得![]() 成立?若存在,請求出所有滿足條件的
成立?若存在,請求出所有滿足條件的![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,見解析
,見解析
【解析】
(1)由條件,可得![]() ,從而可得{
,從而可得{![]() }是公比為
}是公比為![]() 的等比數列,由此可求數列{an}的通項公式;
的等比數列,由此可求數列{an}的通項公式;
(2)由數列的錯位相減法求和,以及等比數列的求和公式,可得所求和.
(3)先通過列舉法寫出{Sn}的前8項,再對m,n的奇偶分類討論,利用{Sn}的單調性來說明僅有一對符合題意的m,n.
(1)由已知可得:![]() ,即
,即![]() ,
,
所以數列![]() 是等比數列,其中首項為
是等比數列,其中首項為![]() ,公比為
,公比為![]() ,所以
,所以![]() ,即
,即![]() .
.
(2)Tn=1![]() 2
2![]() 3
3![]() n(
n(![]() )n,
)n,
![]() Tn=1
Tn=1![]() 2
2![]() (
(![]() )n
)n![]() n(
n(![]() )n+1,
)n+1,
作差得:![]() Tn=
Tn=![]() n
n![]() n(
n(![]() )n+1=
)n+1=![]() n(
n(![]() )n+1,
)n+1,
所以![]()
(3)由已知可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
1°當![]() 同時為偶數時,可知
同時為偶數時,可知![]() ;設
;設![]() ,則
,則![]() ,因為
,因為
![]()
![]() ,
,
所以數列![]() 單調遞增,則
單調遞增,則![]() ≥5時,
≥5時,![]() ,即{S2n}在
,即{S2n}在![]() ≥5時單調增,所以
≥5時單調增,所以![]() 不成立;
不成立;
故當![]() 同時為偶數時,可知
同時為偶數時,可知![]() ;
;
2°當![]() 同時為奇數時,設
同時為奇數時,設![]() ,則
,則![]() ,因為
,因為
![]()
![]() ,
,
所以數列![]() 單調遞增,則當
單調遞增,則當![]() ≥2時,
≥2時,![]() ,
,
即![]() ≥2時,
≥2時,![]() ,數列
,數列![]() 在
在![]() ≥2時單調遞增,
≥2時單調遞增,
而![]() ,
,![]() ,
,![]() ,故當
,故當![]() 同時為奇數時,
同時為奇數時,![]() 不成立;
不成立;
3°當![]() 為偶數,
為偶數,![]() 為奇數時,顯然
為奇數時,顯然![]() 時,
時,![]() 不成立,
不成立,
若![]() ,則
,則![]() ,
,
∵![]() ,∴
,∴![]() ,由2°可知
,由2°可知![]() ,∴
,∴![]() ,
,
∴當![]() 為偶數,
為偶數,![]() 為奇數時,
為奇數時,![]() 不成立;
不成立;
4°當![]() 為奇數,
為奇數,![]() 為偶數時,顯然
為偶數時,顯然![]() 時,
時,![]() 不成立,若
不成立,若![]() ,則
,則![]() ,
,
若![]() ,則
,則![]() ,
,
即![]() ,∴
,∴![]() 時,
時,![]() 不成立;
不成立;
若![]() ,由1°知
,由1°知![]() ,又記
,又記![]() 滿足
滿足![]() ,所以
,所以![]() 單調遞增,
單調遞增,![]() ,所以
,所以![]() 時,
時,![]() 不成立;
不成立;
綜上:存在![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,函數
,函數![]() 的圖象在點
的圖象在點![]() 處的切線平行于
處的切線平行于![]() 軸.
軸.
(1)求![]() 的值;
的值;
(2)求函數![]() 的極小值;
的極小值;
(3)設斜率為![]() 的直線與函數
的直線與函數![]() 的圖象交于兩點
的圖象交于兩點![]() ,
, ![]() ,
, ![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,部分對應值如下表,
,部分對應值如下表,![]() 的導函數
的導函數![]() 的圖象如圖所示.
的圖象如圖所示.
|
|
|
|
|
|
|
|
|
|

下列關于![]() 的命題:
的命題:
①函數![]() 的極大值點為
的極大值點為![]() ;
;
②函數![]() 在
在![]() 上是減函數;
上是減函數;
③如果當![]() 時,
時,![]() 的最大值是
的最大值是![]() ,那么
,那么![]() 的最大值為
的最大值為![]() ;
;
④當![]() 時,函數
時,函數![]() 有
有![]() 個零點;
個零點;
⑤函數![]() 的零點個數可能為
的零點個數可能為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 個.
個.
其中正確命題的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設圓![]() 的圓心為
的圓心為![]() ,直線
,直線![]() 過點
過點![]() 且與
且與![]() 軸不重合,直線
軸不重合,直線![]() 交圓
交圓![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() .
.
(1)證明![]() 為定值,并寫出點
為定值,并寫出點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 且與直線
且與直線![]() 垂直的直線與圓
垂直的直線與圓![]() 交于
交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校響應教育部門疫情期間“停課不停學”的號召,實施網絡授課,為檢驗學生上網課的效果,高三學年進行了一次網絡模擬考試.全學年共1500人,現從中抽取了100人的數學成績,繪制成頻率分布直方圖(如圖所示).已知這100人中![]() 分數段的人數比
分數段的人數比![]() 分數段的人數多6人.
分數段的人數多6人.
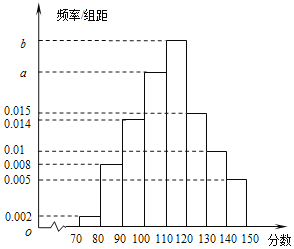
(1)根據頻率分布直方圖,求a,b的值,并估計抽取的100名同學數學成績的中位數;(中位數保留兩位小數)
(2)現用分層抽樣的方法從分數在![]() ,
,![]() 的兩組同學中隨機抽取6名同學,從這6名同學中再任選2名同學作為“網絡課堂學習優秀代表”發言,求這2名同學的分數不在同一組內的概率.
的兩組同學中隨機抽取6名同學,從這6名同學中再任選2名同學作為“網絡課堂學習優秀代表”發言,求這2名同學的分數不在同一組內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】乒乓球賽規定:一局比賽,雙方比分在10平前,一方連續發球2次后,對方再連續發球2次,依次輪換,每次發球,勝方得1分,負方得0分。設在甲、乙的比賽中,每次發球,甲發球得1分的概率為![]() ,乙發球得1分的概率為
,乙發球得1分的概率為![]() ,各次發球的勝負結果相互獨立,甲、乙的一局比賽中,甲先發球.則開始第4次發球時,甲、乙的比分為1比2的概率為________.
,各次發球的勝負結果相互獨立,甲、乙的一局比賽中,甲先發球.則開始第4次發球時,甲、乙的比分為1比2的概率為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秸稈還田是當今世界上普通重視的一項培肥地力的增產措施,在杜絕了秸稈焚燒所造成的大氣污染的同時還有增肥增產作用.某農機戶為了達到在收割的同時讓秸稈還田,花![]() 元購買了一臺新型聯合收割機,每年用于收割可以收入
元購買了一臺新型聯合收割機,每年用于收割可以收入![]() 萬元(已減去所用柴油費);該收割機每年都要定期進行維修保養,第一年由廠方免費維修保養,第二年及以后由該農機戶付費維修保養,所付費用
萬元(已減去所用柴油費);該收割機每年都要定期進行維修保養,第一年由廠方免費維修保養,第二年及以后由該農機戶付費維修保養,所付費用![]() (元)與使用年數
(元)與使用年數![]() 的關系為:
的關系為:![]() ,已知第二年付費
,已知第二年付費![]() 元,第五年付費
元,第五年付費![]() 元.
元.
(1)試求出該農機戶用于維修保養的費用![]() (元)與使用年數
(元)與使用年數![]() 的函數關系;
的函數關系;
(2)這臺收割機使用多少年,可使平均收益最大?(收益=收入-維修保養費用-購買機械費用)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com