
【題目】已知數(shù)列![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,其中
,其中![]() ,則稱
,則稱![]() 為
為![]() 的“生成數(shù)列”.
的“生成數(shù)列”.
(1)若數(shù)列![]() 的“生成數(shù)列”是
的“生成數(shù)列”是![]() ,求
,求![]() ;
;
(2)若![]() 為偶數(shù),且
為偶數(shù),且![]() 的“生成數(shù)列”是
的“生成數(shù)列”是![]() ,證明:
,證明:![]() 的“生成數(shù)列”是
的“生成數(shù)列”是![]() ;
;
(3)若![]() 為奇數(shù),且
為奇數(shù),且![]() 的“生成數(shù)列”是
的“生成數(shù)列”是![]() ,
,![]() 的“生成數(shù)列”是
的“生成數(shù)列”是![]() ,…,依次將數(shù)列
,…,依次將數(shù)列![]() ,
,![]() ,
,![]() ,…的第
,…的第![]() 項(xiàng)取出,構(gòu)成數(shù)列
項(xiàng)取出,構(gòu)成數(shù)列![]() .
.
探究:數(shù)列![]() 是否為等比數(shù)列,并說明理由.
是否為等比數(shù)列,并說明理由.
【答案】(1)![]() ;(2)見解析;(3)見解析
;(2)見解析;(3)見解析
【解析】
試題(1)解:![]() ,
,![]() ,同理,
,同理,![]() ;(2)只需按照定義證明即可,證明:
;(2)只需按照定義證明即可,證明:![]() ,
,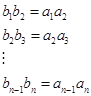 ∵
∵![]() 為偶數(shù),將上述
為偶數(shù),將上述![]() 個(gè)等式中第2,4,6, ,
個(gè)等式中第2,4,6, ,![]() 這
這![]() 個(gè)式子兩邊取倒數(shù),再將這
個(gè)式子兩邊取倒數(shù),再將這![]() 個(gè)式子相乘得:
個(gè)式子相乘得:![]()
![]() ,
,![]() 因?yàn)?/span>
因?yàn)?/span>![]() ,
,![]() ,所以根據(jù)“生成數(shù)列”的定義,數(shù)列
,所以根據(jù)“生成數(shù)列”的定義,數(shù)列![]() 是數(shù)列
是數(shù)列![]() 的“生成數(shù)列”;(3)因?yàn)?/span>
的“生成數(shù)列”;(3)因?yàn)?/span>![]() ,所以
,所以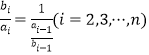 .
.
所以欲證![]() 成等差數(shù)列,只需證明
成等差數(shù)列,只需證明![]() 成等差數(shù)列即可.
成等差數(shù)列即可.
試題解析:(1)解:![]() ,
,![]()
同理,![]() . 4分
. 4分
(寫對(duì)一個(gè)![]() 得1分,總分4分)
得1分,總分4分)
(2)證明:![]()
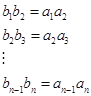 7分
7分
∵![]() 為偶數(shù),將上述
為偶數(shù),將上述![]() 個(gè)等式中第2,4,6, ,
個(gè)等式中第2,4,6, ,![]() 這
這![]() 個(gè)式子兩邊取倒數(shù),再將這
個(gè)式子兩邊取倒數(shù),再將這![]() 個(gè)式子相乘得:
個(gè)式子相乘得:![]()
∴![]() 9分
9分
因?yàn)?/span>![]() ,
,![]()
所以根據(jù)“生成數(shù)列”的定義,數(shù)列![]() 是數(shù)列
是數(shù)列![]() 的“生成數(shù)列”. 10分
的“生成數(shù)列”. 10分
(3)證明:因?yàn)?/span>![]() ,
,
所以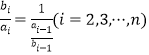 .
.
所以欲證![]() 成等差數(shù)列,只需證明
成等差數(shù)列,只需證明![]() 成等差數(shù)列即可. 12分
成等差數(shù)列即可. 12分
對(duì)于數(shù)列![]() 及其“生成數(shù)列”
及其“生成數(shù)列”![]()
![]()
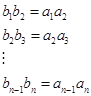
∵![]() 為奇數(shù),將上述
為奇數(shù),將上述![]() 個(gè)等式中第2,4,6, ,
個(gè)等式中第2,4,6, ,![]() 這
這![]() 個(gè)式子兩邊取倒數(shù),再將這
個(gè)式子兩邊取倒數(shù),再將這![]() 個(gè)式子相乘得:
個(gè)式子相乘得:
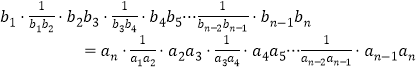
∴![]()
因?yàn)?/span>![]() ,
,![]()
數(shù)列![]() 的“生成數(shù)列”為
的“生成數(shù)列”為![]() ,因?yàn)?/span>
,因?yàn)?/span>![]()
所以![]() 成對(duì)比數(shù)列.
成對(duì)比數(shù)列.
同理可證,![]() 也成等比數(shù)列.即
也成等比數(shù)列.即![]() 是等比數(shù)列.
是等比數(shù)列.
所以![]() 成等差數(shù)列. 16分
成等差數(shù)列. 16分



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
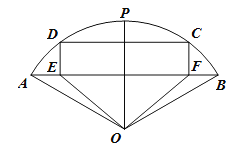
【題目】有一塊圓心角為120度,半徑為![]() 的扇形鋼板
的扇形鋼板![]() (
(![]() 為弧
為弧![]() 的中點(diǎn)),現(xiàn)要將其裁剪成一個(gè)五邊形磨具
的中點(diǎn)),現(xiàn)要將其裁剪成一個(gè)五邊形磨具![]() ,其下部為等腰三角形
,其下部為等腰三角形![]() ,上部為矩形
,上部為矩形![]() .設(shè)
.設(shè)![]() 五邊形
五邊形![]() 的面積為
的面積為![]() .
.
(1)寫出![]() 關(guān)于
關(guān)于![]() 的函數(shù)表達(dá)式,并寫出
的函數(shù)表達(dá)式,并寫出![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 取得最大值時(shí),求
取得最大值時(shí),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
(1)證明:![]() 平面
平面![]() ;
;
(2)若點(diǎn)![]() 在棱
在棱![]() 上,且
上,且![]() ,求點(diǎn)
,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國高鐵的快速發(fā)展給群眾出行帶來巨大便利,極大促進(jìn)了區(qū)域經(jīng)濟(jì)社會(huì)發(fā)展.已知某條高鐵線路通車后,發(fā)車時(shí)間間隔![]() (單位:分鐘)滿足
(單位:分鐘)滿足![]() ,經(jīng)測算,高鐵的載客量與發(fā)車時(shí)間間隔
,經(jīng)測算,高鐵的載客量與發(fā)車時(shí)間間隔![]() 相關(guān):當(dāng)
相關(guān):當(dāng)![]() 時(shí)高鐵為滿載狀態(tài),載客量為
時(shí)高鐵為滿載狀態(tài),載客量為![]() 人;當(dāng)
人;當(dāng)![]() 時(shí),載客量會(huì)在滿載基礎(chǔ)上減少,減少的人數(shù)與
時(shí),載客量會(huì)在滿載基礎(chǔ)上減少,減少的人數(shù)與![]() 成正比,且發(fā)車時(shí)間間隔為
成正比,且發(fā)車時(shí)間間隔為![]() 分鐘時(shí)的載客量為
分鐘時(shí)的載客量為![]() 人.記發(fā)車間隔為
人.記發(fā)車間隔為![]() 分鐘時(shí),高鐵載客量為
分鐘時(shí),高鐵載客量為![]() .
.
![]() 求
求![]() 的表達(dá)式;
的表達(dá)式;
![]() 若該線路發(fā)車時(shí)間間隔為
若該線路發(fā)車時(shí)間間隔為![]() 分鐘時(shí)的凈收益
分鐘時(shí)的凈收益![]() (元),當(dāng)發(fā)車時(shí)間間隔為多少時(shí),單位時(shí)間的凈收益
(元),當(dāng)發(fā)車時(shí)間間隔為多少時(shí),單位時(shí)間的凈收益![]() 最大?
最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國際上鉆石的重量計(jì)量單位為克拉;已知某種鉆石的價(jià)值![]() (美元)與其重量
(美元)與其重量![]() (克拉)的平方成正比,且一顆重為3克拉的該種鉆石的價(jià)值為54000美元;
(克拉)的平方成正比,且一顆重為3克拉的該種鉆石的價(jià)值為54000美元;
(1)寫出![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)若把一顆鉆石切割成重量比為![]() 的兩顆鉆石,求價(jià)值損失的百分率;
的兩顆鉆石,求價(jià)值損失的百分率;
(3)把一顆鉆石切割成兩顆鉆石,若兩顆鉆石的重量分別為![]() 克拉和
克拉和![]() 克拉,試用你所學(xué)的數(shù)學(xué)知識(shí)分析當(dāng)
克拉,試用你所學(xué)的數(shù)學(xué)知識(shí)分析當(dāng)![]() ,
,![]() 滿足何種關(guān)系時(shí),價(jià)值損失的百分率最大.
滿足何種關(guān)系時(shí),價(jià)值損失的百分率最大.
(注:價(jià)值損失的百分率![]() ,在切割過程中重量損耗忽略不計(jì))
,在切割過程中重量損耗忽略不計(jì))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
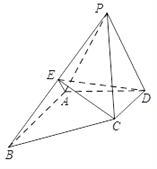
【題目】如圖,四棱錐![]() 中,
中, ![]() 為正三角形,
為正三角形, ![]() ,
, ![]() 為棱
為棱![]() 的中點(diǎn).
的中點(diǎn).
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一商場對(duì)5年來春節(jié)期間服裝類商品的優(yōu)惠金額![]() (單位:萬元)與銷售額
(單位:萬元)與銷售額![]() (單位:萬元)之間的關(guān)系進(jìn)行分析研究并做了記錄,得到如下表格.
(單位:萬元)之間的關(guān)系進(jìn)行分析研究并做了記錄,得到如下表格.
日期 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)畫出散點(diǎn)圖,并判斷服裝類商品的優(yōu)惠金額與銷售額是正相關(guān)還是負(fù)相關(guān);

(2)根據(jù)表中提供的數(shù)據(jù),求出![]() 與
與![]() 的回歸方程
的回歸方程![]() ;
;
(3)若2019年春節(jié)期間商場預(yù)定的服裝類商品的優(yōu)惠金額為10萬元,估計(jì)該商場服裝類商品的銷售額.
參考公式:
參考數(shù)據(jù):![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l方程為(m+2)x﹣(m+1)y﹣3m﹣7=0,m∈R.
(1)求證:直線l恒過定點(diǎn)P,并求出定點(diǎn)P的坐標(biāo);
(2)若直線l在x軸,y軸上的截距相等,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓M與直線![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,圓心M在x軸上.
,圓心M在x軸上.
(1)求圓M的方程;
(2)過點(diǎn)M且不與x軸重合的直線與圓M相交于A,B兩點(diǎn),O為坐標(biāo)原點(diǎn),直線OA,OB分別與直線x=8相交于C,D兩點(diǎn),記△OAB、△OCD的面積分別是S1、S2.求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com