
【題目】已知函數![]() (其中
(其中![]() 是常數,且
是常數,且![]() ),曲線
),曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然對數的底),使得
是自然對數的底),使得![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若對任意
,若對任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]()
【解析】
(1)求出![]() 在
在![]() 處的導數,利用斜率和函數值建立等式關系,則可求出
處的導數,利用斜率和函數值建立等式關系,則可求出![]() 的值. (2)由條件可知,原題等價于
的值. (2)由條件可知,原題等價于![]() 在
在![]() 上有解,設
上有解,設![]() ,即
,即![]() ,求導求函數的最值,從而求出
,求導求函數的最值,從而求出![]() 的取值范圍. (3)通過求導分析
的取值范圍. (3)通過求導分析![]() 的單調性和最值,分類討論求出
的單調性和最值,分類討論求出![]() 的取值范圍.
的取值范圍.
(1)![]() ,由題知
,由題知![]() ,且
,且![]() ,
,
解得![]() ;
;
(2)由(1)知![]() ,因為存在
,因為存在![]() ,使得
,使得![]() ,
,
即![]() ,設
,設![]() ,則需
,則需![]() ,
,
![]() ,設
,設![]() ,則
,則![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 單調遞增,又因為
單調遞增,又因為![]() ,所以
,所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 單調遞增,所以
單調遞增,所以![]() ,
,
令![]() ,解得
,解得![]() ;
;
(3)![]() ,
,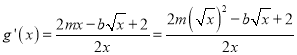 ,
,
①當![]() 時,對任意
時,對任意![]() ,易知方程
,易知方程![]() 均僅有唯一解
均僅有唯一解![]() ,
,
且當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
故方程![]() 最多有兩個不同的實數解,所以
最多有兩個不同的實數解,所以![]() 不符合題意;
不符合題意;
② 當![]() 時,若
時,若![]() ,則
,則![]() 恒成立,
恒成立,![]() 單調遞增,
單調遞增,
方程![]() 最多只有一個實數解,不符題意,
最多只有一個實數解,不符題意,
所以對任意![]() ,應有
,應有![]() ,即
,即![]() ,
,
此時,易知方程![]() 在
在![]() 上有兩個不同的實數根
上有兩個不同的實數根![]() ,
,
因為![]() ,不妨取
,不妨取![]() ,則有
,則有![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 極大值 |
| 極小值 |
|
由表可知,![]() 的極大值為
的極大值為![]() ,
,
因為![]() ,所以
,所以![]() ,
,
又因為![]() ,且
,且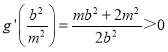 ,所以
,所以![]() ,
,
因為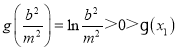 ,所以必然存在
,所以必然存在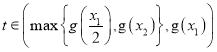 ,
,
使得方程![]() 在區間
在區間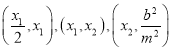 上均有一個實數解,符合題意;
上均有一個實數解,符合題意;
綜上所述,實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
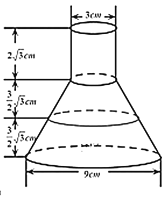
【題目】《烏鴉喝水》是《伊索寓言》中一個寓言故事,通過講述已知烏鴉喝水的故事,告訴人們遇到困難要運用智慧,認真思考才能讓問題迎刃而解的道理,如圖![]() 所示,烏鴉想喝水,發現有一個錐形瓶,上面部分是圓柱體,下面部分是圓臺,瓶口直徑為
所示,烏鴉想喝水,發現有一個錐形瓶,上面部分是圓柱體,下面部分是圓臺,瓶口直徑為![]() 厘米,瓶底直徑為
厘米,瓶底直徑為![]() 厘米,瓶口距瓶頸為
厘米,瓶口距瓶頸為![]() 厘米,瓶頸到水位線距離和水位線到瓶底距離均為
厘米,瓶頸到水位線距離和水位線到瓶底距離均為![]() 厘米,現將
厘米,現將![]() 顆石子投入瓶中,發現水位線上移
顆石子投入瓶中,發現水位線上移![]() 厘米,若只有當水位線到達瓶口時烏鴉才能喝到水,則烏鴉共需要投入的石子數量至少是( )
厘米,若只有當水位線到達瓶口時烏鴉才能喝到水,則烏鴉共需要投入的石子數量至少是( )
A.![]() 顆B.
顆B.![]() 顆C.
顆C.![]() 顆D.
顆D.![]() 顆
顆
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市一中學高三年級統計學生的最近20次數學周測成績(滿分150分),現有甲乙兩位同學的20次成績如莖葉圖所示:
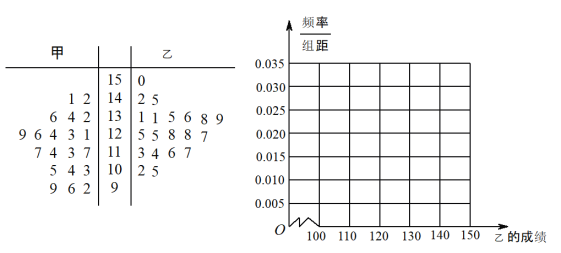
(1)根據莖葉圖求甲乙兩位同學成績的中位數,并據此判斷甲乙兩位同學的成績誰更好?
(2)將同學乙的成績的頻率分布直方圖補充完整;
(3)現從甲乙兩位同學的不低于140分的成績中任意選出2個成績,設選出的2個成績中含甲的成績的個數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在橢圓![]() 上任取一點
上任取一點![]() (
(![]() 不為長軸端點),連結
不為長軸端點),連結![]() 、
、![]() ,并延長與橢圓
,并延長與橢圓![]() 分別交于點
分別交于點![]() 、
、![]() 兩點,已知
兩點,已知![]() 的周長為8,
的周長為8,![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設坐標原點為![]() ,當
,當![]() 不是橢圓的頂點時,直線
不是橢圓的頂點時,直線![]() 和直線
和直線![]() 的斜率之積是否為定值?若是定值,請求出這個定值;若不是定值,請說明理由.
的斜率之積是否為定值?若是定值,請求出這個定值;若不是定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
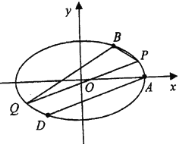
【題目】已知橢圓![]() :
:![]() 的右頂點為
的右頂點為![]() ,離心率為
,離心率為![]() ,點
,點![]() 在橢圓上,點
在橢圓上,點![]() 與點
與點![]() 關于原點對稱.
關于原點對稱.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)求經過點![]() ,
,![]() 且和
且和![]() 軸相切的圓的方程;
軸相切的圓的方程;
(3)若![]() ,
,![]() 是橢圓上異于
是橢圓上異于![]() ,
,![]() 的兩個點,且
的兩個點,且![]() ,點
,點![]() 在直線
在直線![]() 的上方,試判斷
的上方,試判斷![]() 的平分線是否經過
的平分線是否經過![]() 軸上的一個定點?若是,求出該定點坐標;若不是,請說明理由.
軸上的一個定點?若是,求出該定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春,新型冠狀病毒在我國湖北武漢爆發并訊速蔓延,病毒傳染性強并嚴重危害人民生命安全,國家衛健委果斷要求全體人民自我居家隔離,為支援湖北武漢新型冠狀病毒疫情防控工作,各地醫護人員紛紛逆行,才使得病毒蔓延得到了有效控制.某社區為保障居民的生活不受影響,由社區志愿者為其配送蔬菜、大米等生活用品,記者隨機抽查了男、女居民各100名對志愿者所買生活用品滿意度的評價,得到下面的2×2列聯表.
特別滿意 | 基本滿意 | |
男 | 80 | 20 |
女 | 95 | 5 |
(1)被調查的男性居民中有5個年輕人,其中有2名對志愿者所買生活用品特別滿意,現在這5名年輕人中隨機抽取3人,求至多有1人特別滿意的概率.
(2)能否有99%的把握認為男、女居民對志愿者所買生活用品的評價有差異?
附: 
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】嫦娥四號月球探測器于2018年12月8日搭載長征三號乙運載火箭在西昌衛星發射中心發射.12日下午4點43分左右,嫦娥四號順利進入了以月球球心為一個焦點的橢圓形軌道,如圖中③所示,其近月點與月球表面距離為100公里,遠月點與月球表面距離為400公里,已知月球的直徑約為3476公里,對該橢圓有下述四個結論:
(1)焦距長約為300公里;
(2)長軸長約為3988公里;
(3)兩焦點坐標約為![]() ;
;
(4)離心率約為![]() .
.
其中正確結論的個數為( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() ,
,![]() ,則下面結論正確的是( )
,則下面結論正確的是( )
A.把![]() 上各點的橫坐標縮短到原來的
上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向右平移
倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
B.把![]() 上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移
上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
C.把![]() 上各點的橫坐標縮短到原來的
上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向左平移
倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
D.把![]() 上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向左平移
上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com