【題目】在△ABC中，a，b，c分別是角A，B，C的對邊， 
= 
，且a+c=2．
（1）求角B；
（2）求邊長b的最小值．
【答案】
（1）解：在△ABC中，由已知 
，
即cosCsinB=（2sinA﹣sinC）cosB，
sin（B+C）=2sinAcosB，sinA=2sinAcosB，
△ABC 中，sinA≠0，
故 
．
（2）解：a+c=2，
由（1） 
，因此b2=a2+c2﹣2accosB=a2+c2﹣ac
由已知b2=（a+c）2﹣3ac=4﹣3ac
故b 的最小值為1．
【解析】（1）利用正弦定理化簡表達式，求角B；個兩角和與差的三角函數化簡求解即可．（2）利用余弦定理求邊長b的最小值．推出b的表達式，利用基本不等式求解即可．
【考點精析】通過靈活運用正弦定理的定義，掌握正弦定理:
即可以解答此題．
科目：高中數學 來源： 題型：
【題目】已知拋物線C：y2=4x，過焦點F作與x軸垂直的直線l1 ， C上任意一點P（x0 ， y0）（y0≠0）處的切線為l，l與l1交于M，l與準線交于N，則 
= ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C對應的邊分別是a，b，c，已知cos2A﹣3cos（B+C）=1． （Ⅰ）求角A的大小；
（Ⅱ）若△ABC的面積S=5 
，b=5，求sinBsinC的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，PD⊥平面ABCD，AB∥CD，∠ADC=90°，PD=AD=AB=1，DC=2．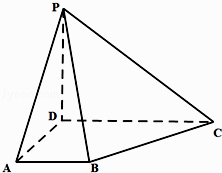 
（1）求證：BC⊥平面PBD；
（2）求二面角A﹣PB﹣C的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的多面體，它的正視圖為直角三角形，側視圖為正三角形，俯視圖為正方形（尺寸如圖所示），E為VB的中點． 
（1）求證：VD∥平面EAC；
（2）求二面角A﹣VB﹣D的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線E的中心為原點，P（3，0）是E的焦點，過P的直線l與E相交于A，B兩點，且AB的中點為N（﹣12，﹣15），則E的方程式為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設集合A={x|x2+2x﹣3＜0}，集合B={x||x+a|＜1}．
（1）若a=3，求A∪B；
（2）設命題p：x∈A，命題q：x∈B，若p是q成立的必要不充分條件，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
