【題目】已知函數
滿足
，對于任意
，且
.令
.
（1）求函數
解析式；
（2）探求函數
在區間
上的零點個數.
【答案】（1）
；（2）當
或
時，函數
在
上有一個零點，當
時，函數在上沒有零點.
【解析】
試題分析：（1）由
，得
，由
可知
，以及任意
，可得
，綜合求得；（2）是一分段函數，先討論對稱軸
和
與絕對值零點
的大小，再在每種情況下討論絕對值零點和區間端點的大小關系進行分類討論.
試題解析：（1）由，得，由可知， 所以
，又對于任意，，即
都成立， 所以
，，
，
所以.
（2）
,
若
，
，其對稱軸為，當
，即
時，函數在
上為增函數； 當
，即
時，函數在
上為減函數， 在
上為增函數；若
，
其對稱軸為，此時
， 所以函數在
上為減函數， 在
上為增函數， 且
，所以函數在上有一個零點；當
時 ，
，沒有零點；當
時，函數在
上為增函數， 在
上為減函數，且
，若
，即
時，函數在上沒有零點， 若
，即時， 函數在上有一個零點.綜上得， 當或時函數
在上有一個零點；當時，函數在上沒有零點.
科目：高中數學 來源： 題型：
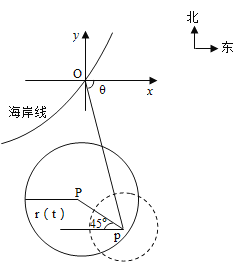
【題目】在某海濱城市附近海面有一臺風，據監測，當前臺風中心位于城市
（如圖）的東偏南
方向300km的海面
處，并以20km/h的速度向西偏北
方向移動，臺風侵襲的范圍為圓形區域，當前半徑為60km，并以10km/h的速度不斷增大，問幾小時后該城市開始受到臺風的侵襲？受到臺風侵襲的時間有多少小時？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C所對的邊分別為a，b，c，已知cos C＋（cos A－
sin A）cos B＝0.
（1）求角B的大小；
（2）若a＋c＝1，求b的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
：
.
（1）直線
過點
，且與圓交于
兩點，若
，求直線的方程；
（2）過圓上一動點
作平行于
軸的直線
，設與
軸的交點為
，若向量
，求動點
的軌跡方程，并說明此軌跡是什么曲線.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知橢圓
的離心率
，長軸長為4.
（1）求橢圓
的方程；
（2）設動直線
與橢圓
有且只有一個公共點
，過右焦點
作直線
與直線
交與點
，且
.求證：點
在定直線上，并求出定直線方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列
的前
項和為
，并且
，數列
滿足：
，記數列
的前
項和為
.
（1）求數列
的通項公式
及前項和為
；
（2）求數列的通項公式
及前項和為
；
（3）記集合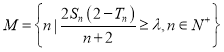
，若
的子集個數為16，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個命題：
①垂直于同一平面的兩條直線相互平行；
②平行于同一平面的兩條直線相互平行；
③若一條直線平行于一個平面內的無數條直線，那么這條直線平行于這個平面；
④若一條直線垂直于一個平面內的任一條直線，那么這條直線垂直于這個平面．
其中真命題的個數是（ ）
A．1個 B．2個 C．3個 D．4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
