
【題目】如圖,在半徑為![]() 的半圓形鐵皮上截取一塊矩形材料ABCD(點A、B在直徑上,點C、D在半圓周上),并將其卷成一個以AD為母線的圓柱體罐子的側面(不計剪裁和拼接損耗),
的半圓形鐵皮上截取一塊矩形材料ABCD(點A、B在直徑上,點C、D在半圓周上),并將其卷成一個以AD為母線的圓柱體罐子的側面(不計剪裁和拼接損耗),
(1)若要求圓柱體罐子的側面積最大,應如何截取?
(2)若要求圓柱體罐子的體積最大,應如何截取?

【答案】(1)當截取的矩形鐵皮的一邊![]() 為
為![]() 為時,圓柱體罐子的側面積最大.
為時,圓柱體罐子的側面積最大.
(2)當截取的矩形鐵皮的一邊![]() 為
為![]() 為時,圓柱體罐子的體積最大.
為時,圓柱體罐子的體積最大.
【解析】解:(1)如圖,設圓心為O,連結![]() ,設
,設![]()
![]() ,
,
法一 易得![]() ,
, ![]() ,故所求矩形
,故所求矩形![]() 的面積為
的面積為 ![]()
![]()
![]()
![]() (
(![]() )
)
(當且僅當![]() ,
, ![]() (
(![]() )時等號成立) 此時
)時等號成立) 此時![]()
![]() ;
;
法二 設![]() ,
, ![]() ; 則
; 則![]() ,
, ![]() ,
,
所以矩形![]() 的面積為
的面積為![]() ,
,
當![]() ,即
,即![]() 時,
時, ![]() (
(![]() )此時
)此時![]()
![]() ;
;
(2)設圓柱的底面半徑為![]() ,體積為
,體積為![]() ,由
,由![]() 得,
得, ![]() ,
,
所以![]() ,其中
,其中![]() ,
,
由![]() 得
得![]() ,此時,
,此時, ![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減, 故當
上單調遞減, 故當![]()
![]() 時,體積最大為
時,體積最大為![]()
![]() ,
,
答:(1)當截取的矩形鐵皮的一邊![]() 為
為![]()
![]() 為時,圓柱體罐子的側面積最大.
為時,圓柱體罐子的側面積最大.
(2)當截取的矩形鐵皮的一邊![]() 為
為![]()
![]() 為時,圓柱體罐子的體積最大.
為時,圓柱體罐子的體積最大.


科目:高中數學 來源: 題型:
【題目】數列{bn}(bn>0)的首項為1,且前n項和Sn滿足Sn﹣Sn﹣1= ![]() +
+ ![]() (n≥2).
(n≥2).
(1)求{bn}的通項公式;
(2)若數列{ ![]() }前n項和為Tn , 問Tn>
}前n項和為Tn , 問Tn> ![]() 的最小正整數n是多少?
的最小正整數n是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C所對的邊分別為a,b,c.向量 ![]() =(a,
=(a, ![]() b)與
b)與 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面積.
,b=2,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個圓心角為直角的扇形![]() 花草房,半徑為1,點
花草房,半徑為1,點![]() 是花草房弧上一個動點,不含端點,現打算在扇形
是花草房弧上一個動點,不含端點,現打算在扇形![]() 內種花,
內種花, ![]() ,垂足為
,垂足為![]() ,
, ![]() 將扇形
將扇形![]() 分成左右兩部分,在
分成左右兩部分,在![]() 左側部分三角形
左側部分三角形![]() 為觀賞區,在
為觀賞區,在![]() 右側部分種草,已知種花的單位面積的造價為
右側部分種草,已知種花的單位面積的造價為![]() ,種草的單位面積的造價為2
,種草的單位面積的造價為2![]() ,其中
,其中![]() 為正常數,設
為正常數,設![]() ,種花的造價與種草的造價的和稱為總造價,不計觀賞區的造價,總造價為
,種花的造價與種草的造價的和稱為總造價,不計觀賞區的造價,總造價為![]()

求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
求當![]() 為何值時,總造價最小,并求出最小值。
為何值時,總造價最小,并求出最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某校高一年級學生參加社區服務次數進行統計,隨機抽取![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
分組 | 頻數 | 頻率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合計 |
| 1 |

(1)求出表中![]() 及圖中
及圖中![]() 的值;
的值;
(2)試估計他們參加社區服務的平均次數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至少1人參加社區服務次數在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的中心在坐標原點,焦點在x軸上,橢圓C上的點到焦點距離的最大值為3,離心率 ![]() .
.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)若經過左焦點F1且傾斜角為 ![]() 的直線l與橢圓交于A、B兩點,求|AB|的值.
的直線l與橢圓交于A、B兩點,求|AB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過△ABC所在平面α外一點P,作PO⊥α,垂足為O,連接PA,PB,PC,若點O是△ABC的內心,則( )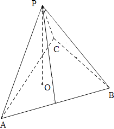
A.PA=PB=PC
B.點P到AB,BC,AC的距離相等
C.PA⊥PB,PB⊥PC,PC⊥PA
D.PA,PB,PC與平面α所成的角相等
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一汽車廠生產![]() 三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛):
三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如下表(單位:輛):
轎車 | 轎車 | 轎車 | |
舒適型 | 100 | 150 |
|
標準型 | 300 | 450 | 600 |
按類用分層抽樣的方法在這個月生產的轎車中抽取50輛,其中有![]() 類轎車10輛.
類轎車10輛.
(I)求![]() 的值;
的值;
(II)用分層抽樣的方法在![]() 類轎車中抽取一個容量為5的樣本.將該樣本看成一個總體,從中任取2輛,求至少有1輛舒適型轎車的概率;
類轎車中抽取一個容量為5的樣本.將該樣本看成一個總體,從中任取2輛,求至少有1輛舒適型轎車的概率;
(III)用隨機抽樣的方法從![]() 類舒適型轎車中抽取8輛,經檢測它們的得分
類舒適型轎車中抽取8輛,經檢測它們的得分![]() 的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把這8輛轎車的得分看成一個總體,從中任取一個數
的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把這8輛轎車的得分看成一個總體,從中任取一個數![]() ,設樣本平均數為
,設樣本平均數為![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com