對于給定數列{cn},如果存在實常數p,q使得cn+1=pcn+q對于任意n∈N*都成立,我們稱數列{cn}是“M類數列”.
(1)若an=2n,bn=3•2n,n∈N*,數列{an}、{bn}是否為“M類數列”?若是,指出它對應的實常數p,q,若不是,請說明理由;
(2)證明:若數列{an}是“M類數列”,則數列{an+an+1}也是“M類數列”;
(3)若數列{an}滿足a1=2,an+an+1=3t•2n(n∈N*),t為常數.求數列{an}前2009項的和.并判斷{an}是否為“M類數列”,說明理由;
(4)根據對(2)(3)問題的研究,對數列{an}的相鄰兩項an、an+1,提出一個條件或結論與“M類數列”概念相關的真命題,并探究其逆命題的真假.
【答案】
分析:本題考查的知識點是演繹推理和類比推理.(1)的解題思路是判斷a
n,b
n是否滿足“M類數列”的定義:存在實常數p,q使得c
n+1=pc
n+q對于任意n∈N
*都成立.找到常數p、q是解決問題的關鍵.(2)是看數列{a
n+a
n+1}是否也滿足“M類數列”的定義,根據已知想辦法將數列{a
n+a
n+1}的通項公式轉化為“M類數列”的一般形式.(3)要先求出數列{a
n}的通項公式,然后利用(1)的解法解決問題.(4)是要根據(2)、(3)的結論,進行歸納,大膽猜想出一個與“M類數列”相關的真命題,原則是盡可能的要簡單,以便后續的證明.
解答:解:(1)因為a
n=2n,則有a
n+1=a
n=+2,n∈N
*,
故數列{a
n}是“M類數列”,對應的實常數分別為1,2.
因為b
n=3•2
n,則有b
n+1=2b
n,n∈N
*,
故數列{b
n}是“M類數列”,對應的實常數分別為2,0.
證明:(2)若數列{a
n}是“M類數列”,則存在實常數p,q,
使得a
n+1=pa
n+q對于任意n∈N
*都成立,
且有a
n+2=pa
n+1+q對于任意n∈N
*都成立,
因此(a
n+1+a
n+2)=p(a
n+a
n+1)+2q對于任意n∈N
*都成立,
故數列{a
n+a
n+1}也是“M類數列”.
對應的實常數分別為p,2q.
解:(3)因為a
n+a
n+1=3t•2
n(n∈N
*),
則有a
2+a
3=3t•2
2,a
4+a
5=3t•2
4,…,
a
2006+a
2007=3t•2
2006,a
2008+a
2009=3t•2
2008,
數列{a
n}前2009項的和S
2009=a
1+(a
2+a
3)+(a
4+a
5)+…+(a
2006+a
2007)+(a
2008+a
2009)
=2+3t•2
2+3t•2
4+…+3t•2
2006+3t•2
2008=2+t(2
2010-4),
若數列{a
n}是“M類數列”,則存在實常數p,q
使得a
n+1=pa
n+q對于任意n∈N
*都成立,
且有a
n+2=pa
n+1+q對于任意n∈N
*都成立
因此(a
n+1+a
n+2)=p(a
n+a
n+1)+2q對于任意n∈N
*都成立,
而a
n+a
n+1=3t•2
n(n∈N
*),則有3t•2
n+1=3t•p2
n+2q對于任意n∈N
*,都成立,
可以得到t(p-2)=0,q=0,
①當p=2,q=0時,a
n+1=2a
n,a
n=2
n,t=1,經檢驗滿足條件.
②當t=0,q=0時,a
n+1=-a
n,a
n=2(-1)
n-1,p=-1,經檢驗滿足條件.
因此當且僅當t=1或t=0,時,數列{a
n}也是“M類數列”,對應的實常數分別為2,0,或-1,0.
解:(4)命題一:若數列{a
n}是“M類數列”,則數列{a
n-a
n+1}也是“M類數列”.
逆命題:若數列{a
n-a
n+1}是“M類數列”,則數列{a
n}也是“M類數列”.
當且僅當數列{a
n-a
n+1}是常數列、等比數列時,逆命題是正確的.
命題二:若數列{a
n}是等比數列,則數列{a
n+a
n+1}、{a
n-a
n+1}、{a
n•a
n+1}、
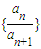
是“M類數列”
逆命題:若數列{a
n+a
n+1}、{a
n-a
n+1}、{a
n•a
n+1}、
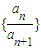
是“M類數列”則數列{a
n}是等比數列.
逆命題是正確的.
點評:歸納推理的一般步驟是:(1)通過觀察個別情況發現某些相同性質;(2)從已知的相同性質中推出一個明確表達的一般性命題(猜想).類比推理的一般步驟是:(1)找出兩類事物之間的相似性或一致性;(2)用一類事物的性質去推測另一類事物的性質,得出一個明確的命題(猜想).演繹推理的主要形式就是由大前提、小前提推出結論的三段論推理.三段論推理的依據用集合論的觀點來講就是:若集合M的所有元素都具有性質P,S是M的子集,那么S中所有元素都具有性質P.

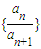 是“M類數列”
是“M類數列”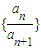 是“M類數列”則數列{an}是等比數列.
是“M類數列”則數列{an}是等比數列.
