
【題目】在△ABC中,角A,B,C的對(duì)邊分別為a,b,c,A=60°,a=3.
(1)若b=2,求cosB;
(2)求△ABC的面積的最大值.
【答案】
(1)解:∵ ![]() ,∴
,∴ ![]() =
= ![]() ,可得,
,可得, ![]()
又∵a>b,
∴A>B,可得B為銳角,
∴ ![]()
(2)解: ![]() ,
,
∵ ![]() ,
,
∴bc=b2+c2﹣9≥2bc﹣9,
∴得bc≤9,當(dāng)且僅當(dāng)b=c時(shí)等號(hào)成立,
∴故S△ABC= ![]() bcsinA≤
bcsinA≤ ![]() 9×
9× ![]() =
= ![]() ,即△ABC的面積的最大值為
,即△ABC的面積的最大值為 ![]()
【解析】(1)由已知利用正弦定理可求sinB的值,利用大邊對(duì)大角可求B為銳角,利用同角三角函數(shù)基本關(guān)系式即可求得cosB的值.(2)由已知及余弦定理,基本不等式可求bc≤9,利用三角形面積公式可求△ABC的面積的最大值.
【考點(diǎn)精析】關(guān)于本題考查的正弦定理的定義和余弦定理的定義,需要了解正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能得出正確答案.
才能得出正確答案.


 小學(xué)學(xué)習(xí)好幫手系列答案
小學(xué)學(xué)習(xí)好幫手系列答案 小學(xué)同步三練核心密卷系列答案
小學(xué)同步三練核心密卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
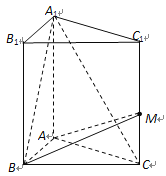
【題目】直三棱柱![]() 中,底面
中,底面![]() 為等腰直角三角形,
為等腰直角三角形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是側(cè)棱
是側(cè)棱![]() 上一點(diǎn),設(shè)
上一點(diǎn),設(shè)![]() .
.
(1) 若![]() ,求
,求![]() 的值;
的值;
(2) 若![]() ,求直線(xiàn)
,求直線(xiàn)![]() 與平面
與平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖莖葉圖記錄了甲、乙兩組各四名同學(xué)的植樹(shù)棵數(shù).乙組記錄中有一個(gè)數(shù)據(jù)模糊,無(wú)法確認(rèn),在圖中以Z表示.
(1)如果Z=8,求乙組同學(xué)植樹(shù)棵數(shù)的平均數(shù)和方差;
(2)如果Z=9,分別從甲、乙兩組中隨機(jī)選取一名同學(xué),求這兩名同學(xué)的植樹(shù)總棵數(shù)為19的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,左、右頂點(diǎn)分別為
,左、右頂點(diǎn)分別為![]() 為直徑的圓O過(guò)橢圓E的上頂點(diǎn)D,直線(xiàn)DB與圓O相交得到的弦長(zhǎng)為
為直徑的圓O過(guò)橢圓E的上頂點(diǎn)D,直線(xiàn)DB與圓O相交得到的弦長(zhǎng)為![]() .設(shè)點(diǎn)
.設(shè)點(diǎn)![]() ,連接PA交橢圓于點(diǎn)C,坐標(biāo)原點(diǎn)為O.
,連接PA交橢圓于點(diǎn)C,坐標(biāo)原點(diǎn)為O.
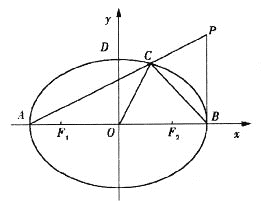
(I)求橢圓E的方程;
(II)若三角形ABC的面積不大于四邊形OBPC的面積,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了迎接珠海作為全國(guó)文明城市的復(fù)查,愛(ài)衛(wèi)會(huì)隨機(jī)抽取了60位路人進(jìn)行問(wèn)卷調(diào)查,調(diào)查項(xiàng)目是自己對(duì)珠海各方面衛(wèi)生情況的滿(mǎn)意度(假設(shè)被問(wèn)卷的路人回答是客觀(guān)的),以分?jǐn)?shù)表示問(wèn)卷結(jié)果,并統(tǒng)計(jì)他們的問(wèn)卷分?jǐn)?shù),把其中不低于50分的分成五段[50,60),[60,70),…[90,100]后畫(huà)出如圖部分頻率分布直方圖,觀(guān)察圖形信息,回答下列問(wèn)題: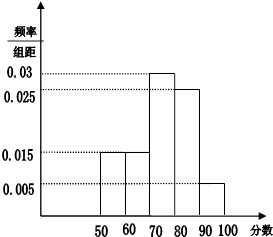
(1)求出問(wèn)卷調(diào)查分?jǐn)?shù)低于50分的被問(wèn)卷人數(shù);
(2)估計(jì)全市市民滿(mǎn)意度在60分及以上的百分比.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列{an}的前n項(xiàng)和為Sn , 且an是Sn與2的等差中項(xiàng),數(shù)列{bn}中,b1=1,點(diǎn)P(bn , bn+1)在直線(xiàn)x﹣y+2=0上.
(1)求a1和a2的值;
(2)求數(shù)列{an},{bn}的通項(xiàng)an和bn;
(3)設(shè)cn=anbn , 求數(shù)列{cn}的前n項(xiàng)和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知f(x)=2+log3x,x∈[1,9],則函數(shù)y=[f(x)]2+f(x2)的最大值為( )
A.6
B.22
C.﹣3
D.13
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】△ABC的內(nèi)角A,B,C的對(duì)邊分別為a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面積為
,△ABC的面積為 ![]() ,求△ABC的周長(zhǎng).
,求△ABC的周長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,側(cè)面PAD⊥底面ABCD,側(cè)棱PA=PD= ![]() ,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn).
,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn). 
(1)求證:PO⊥平面ABCD;
(2)求異面直線(xiàn)PB與CD所成角的余弦值;
(3)線(xiàn)段AD上是否存在點(diǎn)Q,使得它到平面PCD的距離為 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com