
【題目】已知橢圓![]() 1(a>b>0)的左右焦點分別為F1F2,左右頂點分別為AB,上頂點為T,且△TF1F2為等邊三角形.
1(a>b>0)的左右焦點分別為F1F2,左右頂點分別為AB,上頂點為T,且△TF1F2為等邊三角形.
(1)求此橢圓的離心率e;
(2)若直線y=kx+m(k>0)與橢圓交與CD兩點(點D在x軸上方),且與線段F1F2及橢圓短軸分別交于點MN(其中MN不重合),且|CM|=|DN|.
①求k的值;
②設ADBC的斜率分別為k1,k2,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() .(2)①
.(2)①![]() ,②
,②![]()
【解析】
(1)設![]() 的半焦距為c,由題得a=2c,即得橢圓的離心率;(2)①設C(x1,y1),D(x2,y2),聯立直線和橢圓方程得到
的半焦距為c,由題得a=2c,即得橢圓的離心率;(2)①設C(x1,y1),D(x2,y2),聯立直線和橢圓方程得到![]() ,化簡即得解;②先分析得到
,化簡即得解;②先分析得到![]() ,求出
,求出![]() ,進一步分析得到
,進一步分析得到![]() 的取值范圍.
的取值范圍.
(1)設![]() 的半焦距為c,
的半焦距為c,
由△TF1F2為等邊三角形.得a=2c,
即橢圓的離心率![]() ;
;
(2)①設C(x1,y1),D(x2,y2),由y=kx+m,可知![]() ,N(0,m),
,N(0,m),
聯立y=kx+m與![]() ,整理得(a2k2+b2)x2+2kma2x+a2m2﹣a2b2=0,
,整理得(a2k2+b2)x2+2kma2x+a2m2﹣a2b2=0,
其中△=4a2b2(a2k2+b2﹣m2)>0,
易知,x1+x2=xM+xN,即![]() ,
,
解得![]() ,
,
因為,k>0,所以![]() ,
,
②由M在線段F1F2,且M,N不重合,
可知,![]() ,
,
從而![]() ,
,
即![]() ,
,![]() ,并結合在曲線上,則有,
,并結合在曲線上,則有,
所以![]() ,
,
從而可得,![]() ∈
∈![]() ,
,
所以![]() 的取值范圍為
的取值范圍為![]() .
.


 核心素養學練評系列答案
核心素養學練評系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
【題目】
如圖,在直三棱柱![]() 中,平面
中,平面![]() 側面A1ABB1.
側面A1ABB1.
(Ⅰ)求證:![]() ;
;
(Ⅱ)若直線AC與平面A1BC所成的角為θ,二面角A1-BC-A的大小為φ,試判斷θ與φ的大小關系,并予以證明.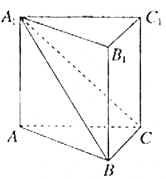
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小學舉辦“父母養育我,我報父母恩”的活動,對六個年級(一年級到六年級的年級代碼分別為1,2…,6)的學生給父母洗腳的百分比y%進行了調查統計,繪制得到下面的散點圖.
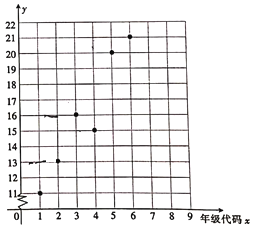
(1)由散點圖看出,可用線性回歸模型擬合y與x的關系,請用相關系數加以說明;
(2)建立y關于x的回歸方程,并據此預計該校學生升入中學的第一年(年級代碼為7)給父母洗腳的百分比.
附注:參考數據:![]()
參考公式:相關系數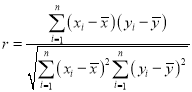 ,若r>0.95,則y與x的線性相關程度相當高,可用線性回歸模型擬合y與x的關系.回歸方程
,若r>0.95,則y與x的線性相關程度相當高,可用線性回歸模型擬合y與x的關系.回歸方程![]() 中斜率與截距的最小二乘估計公式分別為
中斜率與截距的最小二乘估計公式分別為![]() =
=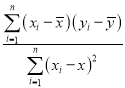 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() 為底面
為底面![]() 的重心.
的重心.
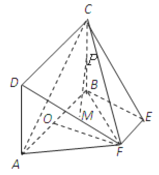
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠銷售部以箱為單位銷售某種零件,每箱的定價為200元,低于100箱按原價銷售;不低于100箱通過雙方議價,買方能以優惠![]() 成交的概率為0.6,以優惠
成交的概率為0.6,以優惠![]() 成交的概率為0.4.
成交的概率為0.4.
(1)甲、乙兩單位都要在該廠購買150箱這種零件,兩單位各自達成的成交價相互獨立,求甲單位優惠比例不低于乙單位優惠比例的概率;
(2)某單位需要這種零件650箱,求購買總價![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
B.命題“若![]() ,則
,則![]() ”的逆否命題為:“若
”的逆否命題為:“若![]() ,則
,則![]() ”
”
C.若![]() 為假命題,則
為假命題,則![]() ,
,![]() 均為假命題
均為假命題
D.命題![]() ,使得
,使得![]() ,則
,則![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠過去在生產過程中將污水直接排放到河流中對沿河環境造成了一定的污染,根據環保部門對該廠過去10年的監測數據,統計出了其每年污水排放量![]() (單位:噸)的頻率分布表:
(單位:噸)的頻率分布表:
污水排放量 |
|
|
|
|
頻率 | 0.1 | 0.3 | 0.4 | 0.2 |
將污水排放量落入各組的頻率作為概率,并假設每年該廠污水排放量相互獨立.
(1)若不加以治理,根據上表中的數據,計算未來3年中至少有2年污水排放量不小于200噸的概率;
(2)根據環保部門的評估,該廠當年污水排放量![]() 時,對沿河環境及經濟造成的損失為5萬元;當年污水排放量
時,對沿河環境及經濟造成的損失為5萬元;當年污水排放量![]() 時,對沿河環境及經濟造成的損失為10萬元;當年污水排放量
時,對沿河環境及經濟造成的損失為10萬元;當年污水排放量![]() 時,對沿河環境及經濟造成的損失為20萬元;當年污水排放量
時,對沿河環境及經濟造成的損失為20萬元;當年污水排放量![]() 時,對沿河環境及經濟造成的損失為50萬元.為了保護環境,減少損失,該廠現有兩種應對方案:
時,對沿河環境及經濟造成的損失為50萬元.為了保護環境,減少損失,該廠現有兩種應對方案:
方案1:若該廠不采取治污措施,則需全部賠償對沿河環境及經濟造成的損失;
方案2:若該廠采購治污設備對所有產生的污水凈化達標后再排放,則不需賠償,采購設備的費用為10萬元,每年設備維護等費用為15萬元,該設備使用10年需重新更換.在接下來的10年里,試比較上述2種方案哪種能為該廠節約資金,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某包子店每天早晨會提前做好若干籠包子,以保證當天及時供應,每賣出一籠包子的利潤為40元,當天未賣出的包子作廢料處理, 每籠虧損20元.該包子店記錄了60天包子的日需求量![]() (單位:籠,
(單位:籠,![]() ),整理得到如圖所示的條形圖,以這60天各需求量的頻率代替相應的概率.
),整理得到如圖所示的條形圖,以這60天各需求量的頻率代替相應的概率.
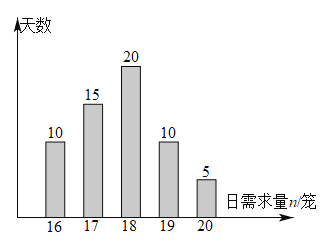
(1)設![]() 為一天的包子需求量,求
為一天的包子需求量,求![]() 的數學期望.
的數學期望.
(2)若該包子店想保證![]() 以上的天數能夠足量供應,則每天至少要做多少籠包子?
以上的天數能夠足量供應,則每天至少要做多少籠包子?
(3)為了減少浪費,該包子店一天只做18籠包子,設![]() 為當天的利潤(單位:元),求
為當天的利潤(單位:元),求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com