
【題目】已知點Pn(an,bn)滿足an+1=an·bn+1,bn+1=![]() (n∈N*),且點P1的坐標(biāo)為(1,-1).
(n∈N*),且點P1的坐標(biāo)為(1,-1).
(1)求過點P1,P2的直線l的方程;
(2)試用數(shù)學(xué)歸納法證明:對于n∈N*,點Pn都在(1)中的直線l上
【答案】(1)2x+y=1(2)證明見解析
【解析】
(1)求出P2的坐標(biāo),列出直線的兩點式方程,化簡即可;
(2)由(1)知,n=1時,2a1+b1=1成立,假設(shè)n=k時,2ak+bk=1成立,進(jìn)而證得當(dāng)n=k+1時,2ak+1+bk+1=1也成立,故n∈N*,Pn都在直線l上.
(1)由題意得a1=1,b1=-1,故b2=![]() ,a2=1×
,a2=1×![]() =
=![]() ,∴P2
,∴P2![]() .
.
∴直線l的方程為 ,即2x+y=1.
,即2x+y=1.
(2)證明:①當(dāng)n=1時,由(1)知,2a1+b1=2×1+(-1)=1成立,
②假設(shè)n=k(k≥1且k∈N*)時,2ak+bk=1成立.
當(dāng)n=k+1時,則![]()
∴當(dāng)n=k+1時,2ak+1+bk+1=1也成立.
由①②知,對于n∈N*,都有2an+bn=1,
即點Pn在直線l上.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
![]() .
.
(1)當(dāng)![]() 時,若函數(shù)
時,若函數(shù)![]() 恰有一個零點,求實數(shù)
恰有一個零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() ,
, ![]() 時,對任意
時,對任意![]() ,有
,有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,以坐標(biāo)原點為極點,
中,以坐標(biāo)原點為極點,![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,點
,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E:![]() (
(![]() )的離心率是
)的離心率是![]() ,
,![]() ,
,![]() 分別為橢圓E的左右頂點,B為上頂點,
分別為橢圓E的左右頂點,B為上頂點,![]() 的面積為2.直線l過點
的面積為2.直線l過點![]() 且與橢圓E交于P,Q兩點(P,Q異于
且與橢圓E交于P,Q兩點(P,Q異于![]() ,
,![]() )
)
(1)求橢圓E的標(biāo)準(zhǔn)方程;
(2)求![]() 的面積最大值;
的面積最大值;
(3)設(shè)直線![]() 與直線
與直線![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,求證:
,求證:![]() 為常數(shù),并求出這個常數(shù).
為常數(shù),并求出這個常數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且sin2A+sin2B+sin2C=sinAsinB+sinBsinC+sinCsin A.
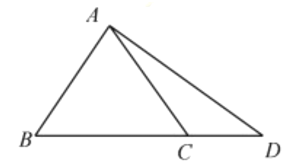
(1)證明:△ABC是正三角形;
(2)如圖,點D在邊BC的延長線上,且BC=2CD,AD![]() ,求sin∠BAD的值.
,求sin∠BAD的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高三課外興趣小組為了了解高三同學(xué)高考結(jié)束后是否打算觀看2018年足球世界杯比賽的情況,從全校高三年級1500名男生、1000名女生中按分層抽樣的方式抽取125名學(xué)生進(jìn)行問卷調(diào)查,情況如下表:
打算觀看 | 不打算觀看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中數(shù)據(jù)b,c;
(2)判斷是否有99%的把握認(rèn)為觀看2018年足球世界杯比賽與性別有關(guān);
(3)在打算觀看2018年足球世界杯比賽的同學(xué)中有5名男生、2名女生來自高三(5)班,從中推選5人接受校園電視臺采訪,請根據(jù)上述方法,求被推選出的5人中恰有四名男生、一名女生的概率.
附:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
![]()
![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標(biāo)原點
的中心在坐標(biāo)原點![]() ,其短半軸長為
,其短半軸長為![]() ,一個焦點坐標(biāo)為
,一個焦點坐標(biāo)為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,點
上,點![]() 在直線
在直線![]() 上的點,且
上的點,且![]() .
.
![]() 證明:直線
證明:直線![]() 與圓
與圓![]() 相切;
相切;
![]() 求
求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過雙曲線![]() 的左焦點
的左焦點![]() 作圓
作圓![]() 的切線交雙曲線的右支于點
的切線交雙曲線的右支于點![]() ,且切點為
,且切點為![]() ,已知
,已知![]() 為坐標(biāo)原點,
為坐標(biāo)原點,![]() 為線段
為線段![]() 的中點(
的中點(![]() 點在切點
點在切點![]() 的右側(cè)),若
的右側(cè)),若![]() 的周長為
的周長為![]() ,則雙曲線的漸近線的方程為( )
,則雙曲線的漸近線的方程為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知A,B是拋物線C:y2=4x上兩點,線段AB的垂直平分線與x軸有唯一的交點P(x0,0).
(1)求證:x0>2;
(2)若直線AB過拋物線C的焦點F,且|AB|=10,求|PF|.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com