
【題目】D為△ABC的BC邊上一點, ![]() ,過D點的直線分別交直線AB、AC于E、F,若
,過D點的直線分別交直線AB、AC于E、F,若 ![]() ,其中λ>0,μ>0,則
,其中λ>0,μ>0,則 ![]() +
+ ![]() = .
= .
【答案】3
【解析】解:如圖所示,
∵ ![]() =
= ![]() +
+ ![]() ,
, ![]() =
= ![]() +
+ ![]() =λ
=λ ![]() ,
,
∴ ![]() =(1﹣λ)
=(1﹣λ) ![]() ;
;
又E,D,F(xiàn)三點共線,
∴存在實數(shù)k,使 ![]() =k
=k ![]() =k(
=k( ![]() ﹣
﹣ ![]() )=kμ
)=kμ ![]() ﹣kλ
﹣kλ ![]() ;
;
又 ![]() =﹣2
=﹣2 ![]() ,
,
∴ ![]() =
= ![]()
![]() =
= ![]()
![]() ﹣
﹣ ![]()
![]() ;
;
∴(1﹣λ) ![]() =(kμ
=(kμ ![]() ﹣kλ
﹣kλ ![]() )﹣(
)﹣( ![]()
![]() ﹣
﹣ ![]()
![]() ),
),
即(1﹣λ) ![]() =(kμ﹣
=(kμ﹣ ![]() )
) ![]() +(
+( ![]() ﹣kλ)
﹣kλ) ![]() ,
,
∴ 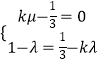 ,
,
解得μ= ![]() ,λ=
,λ= ![]() ;
;
∴ ![]() +
+ ![]() =3(1﹣k)+3k=3.
=3(1﹣k)+3k=3.
所以答案是:3.
所以答案是:3.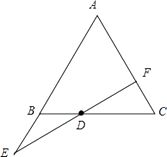
【考點精析】根據(jù)題目的已知條件,利用平面向量的基本定理及其意義的相關(guān)知識可以得到問題的答案,需要掌握如果![]() 、
、![]() 是同一平面內(nèi)的兩個不共線向量,那么對于這一平面內(nèi)的任意向量
是同一平面內(nèi)的兩個不共線向量,那么對于這一平面內(nèi)的任意向量![]() ,有且只有一對實數(shù)
,有且只有一對實數(shù)![]() 、
、![]() ,使
,使![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是⊙O的切線,ADE是⊙O的割線,AC=AB,連接CD,CE,分別與⊙O交于點F,點G. 
(1)求證:△ADC~△ACE;
(2)求證:FG∥AC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知公差不為0的等差數(shù)列![]() 的前三項和為6,且
的前三項和為6,且![]() 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設(shè)![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求使
,求使![]() 的
的![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知兩直線l1:mx+8y+n=0和l2:2x+my-1=0.試確定m,n的值,使
(1)l1與l2相交于點P(m,-1);則m=____,n=_______
(2)l1∥l2.則_________________
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)= ![]() ,關(guān)于x的方程[f(x)]2+mf(x)﹣1=0有三個不同的實數(shù)解,則實數(shù)m的取值范圍是( )
,關(guān)于x的方程[f(x)]2+mf(x)﹣1=0有三個不同的實數(shù)解,則實數(shù)m的取值范圍是( )
A.(﹣∞,e﹣ ![]() )
)
B.(e﹣ ![]() ,+∞)
,+∞)
C.(0,e)
D.(1,e)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 在
在![]() 處有極大值.
處有極大值.
(1)求實數(shù)![]() 的值;
的值;
(2)若關(guān)于![]() 的方程
的方程![]() ,
,![]() 有三個不同的實根,求實數(shù)
有三個不同的實根,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
已知圓![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),若
為參數(shù)),若![]() 是圓
是圓![]() 與
與![]() 軸正半軸的交點,以坐標(biāo)原點
軸正半軸的交點,以坐標(biāo)原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標(biāo)系,設(shè)過點
軸正半軸為極軸,建立極坐標(biāo)系,設(shè)過點![]() 的圓
的圓![]() 的切線為
的切線為![]() .
.
(1)求直線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)求圓![]() 上到直線
上到直線![]() 的距離最大的點的直角坐標(biāo).
的距離最大的點的直角坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】點M(3,2)到拋物線C:y=ax2(a>0)準(zhǔn)線的距離為4,F(xiàn)為拋物線的焦點,點N(l,l),當(dāng)點P在直線l:x﹣y=2上運動時, ![]() 的最小值為( )
的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com