
【題目】一湖中有不在同一直線的三個小島A、B、C,前期為開發旅游資源在A、B、C三島之間已經建有索道供游客觀賞,經測量可知AB兩島之間距離為3公里,BC兩島之間距離為5公里,AC兩島之間距離為7公里,現調查后發現,游客對在同一圓周上三島A、B、C且位于![]() (優弧)一片的風景更加喜歡,但由于環保、安全等其他原因,沒辦法盡可能一次游覽更大面積的湖面風光,現決定在
(優弧)一片的風景更加喜歡,但由于環保、安全等其他原因,沒辦法盡可能一次游覽更大面積的湖面風光,現決定在![]() 上選擇一個點D建立索道供游客游覽,經研究論證為使得游覽面積最大,只需使得△ADC面積最大即可.則當△ADC面積最大時建立索道AD的長為______公里.(注:索道兩端之間的長度視為線段)
上選擇一個點D建立索道供游客游覽,經研究論證為使得游覽面積最大,只需使得△ADC面積最大即可.則當△ADC面積最大時建立索道AD的長為______公里.(注:索道兩端之間的長度視為線段)
【答案】![]()
【解析】
根據題意畫出草圖,根據余弦定理求出![]() 的值,設點
的值,設點![]() 到
到![]() 的距離為
的距離為![]() ,可得
,可得![]() ,分析可知
,分析可知![]() 取最大時,
取最大時,![]() 取最大值,然后再對
取最大值,然后再對![]() 為
為![]() 中點和
中點和![]() 不是
不是![]() 中點兩種情況分析,可得
中點兩種情況分析,可得![]() 的最大值為
的最大值為![]() ,然后再根據圓的有關性質和正弦定理,即可求出結果.
,然后再根據圓的有關性質和正弦定理,即可求出結果.
根據題意可作出![]() 及其外接圓
及其外接圓![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,如下圖:
,如下圖:
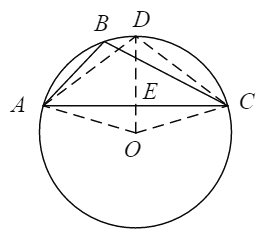
在![]() 中,由余弦定理
中,由余弦定理
![]() ,
,
由![]() 為
為![]() 的內角,可知
的內角,可知![]() ,所以
,所以![]() .
.
設![]() 的半徑為
的半徑為![]() ,點
,點![]() 到
到![]() 的距離為
的距離為![]() ,點
,點![]() 到
到![]() 的距離為
的距離為![]() ,則
,則![]() ,
,
故![]() 取最大時,
取最大時,![]() 取最大值.
取最大值.
①當![]() 為
為![]() 中點時,由垂徑定理知
中點時,由垂徑定理知![]() ,即
,即![]() ,
,
此時![]() ,故
,故![]() ;
;
②當![]() 不是
不是![]() 中點時,
中點時,![]() 不與
不與![]() 垂直,設此時
垂直,設此時![]() 與
與![]() 所成角為
所成角為![]() ,則
,則![]() ,故
,故![]() ;
;
由垂線段最短知![]() ,此時
,此時![]() ;
;
綜上,當![]() 為
為![]() 中點時,
中點時,![]() 到
到![]() 的距離
的距離![]() 最大,最大值為
最大,最大值為![]() ;
;
由圓周角定理可知,![]() ,
,
由垂徑定理知,此時點![]() 為優弧
為優弧![]() 的中點,故
的中點,故![]() ,
,
則![]() ,
,
在![]() 中,由正弦定理得
中,由正弦定理得![]()
所以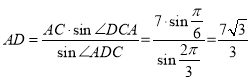 .
.
所以當△ADC面積最大時建立索道AD的長為![]() 公里.
公里.
故答案為:![]() .
.


 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁四名同學組成一個4![]() 100米接力隊,老師要安排他們四人的出場順序,以下是他們四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老師聽了他們四人的對話,安排了一種合理的出場順序,滿足了他們的所有要求,據此我們可以斷定在老師安排的出場順序中跑第三棒的人是( )
100米接力隊,老師要安排他們四人的出場順序,以下是他們四人的要求:甲:我不跑第一棒和第二棒;乙:我不跑第一棒和第四棒;丙:我也不跑第一棒和第四棒;丁:如果乙不跑第二棒,我就不跑第一棒.老師聽了他們四人的對話,安排了一種合理的出場順序,滿足了他們的所有要求,據此我們可以斷定在老師安排的出場順序中跑第三棒的人是( )
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的有_______.(寫出所有正確說法的序號)
①在![]() 中,若
中,若![]() ,則
,則![]() ;
;
②在![]() 中,若
中,若![]() ,則
,則![]() 是銳角三角形;
是銳角三角形;
③在![]() 中,若
中,若![]() ,則
,則![]() ;
;
④若![]() 是等差數列,其前
是等差數列,其前![]() 項和為
項和為![]() ,則三點
,則三點![]()
![]()
![]() 共線;
共線;
⑤等比數列![]() 的前
的前![]() 項和為
項和為![]() ,若對任意的
,若對任意的![]() ,點
,點![]() 均在函數
均在函數![]() (
(![]() 且
且![]() ,
,![]()
![]() 均為常數)的圖象上,則
均為常數)的圖象上,則![]() 的值為
的值為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面結論中,正確結論的是( )
A.存在兩個不等實數![]() ,使得等式
,使得等式![]() 成立
成立
B.![]() (0< x < π)的最小值為4
(0< x < π)的最小值為4
C.若![]() 是等比數列
是等比數列![]() 的前
的前![]() 項的和,則
項的和,則![]() 成等比數列
成等比數列
D.已知![]() 的三個內角
的三個內角![]() 所對的邊分別為
所對的邊分別為![]() ,若
,若![]() ,則
,則![]() 一定是銳角三角形
一定是銳角三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在直角三角形ABC中,![]() ,
,![]() (如右圖所示)
(如右圖所示)
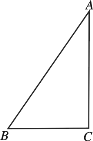
(Ⅰ)若以AC為軸,直角三角形ABC旋轉一周,試說明所得幾何體的結構特征并求所得幾何體的表面積.
(Ⅱ)一只螞蟻在問題(Ⅰ)形成的幾何體上從點B繞著幾何體的側面爬行一周回到點B,求螞蟻爬行的最短距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,已知A,a,b,給出下列說法:
中,已知A,a,b,給出下列說法:
①若![]() ,則此三角形最多有一解;
,則此三角形最多有一解;
②若![]() ,且
,且![]() ,則此三角形為直角三角形,且
,則此三角形為直角三角形,且![]() ;
;
③當![]() ,且
,且![]() 時,此三角形有兩解.
時,此三角形有兩解.
其中正確說法的個數為( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com