【題目】已知等差數列
的前
項和為
，并且
，
，數列
滿足：
，
，記數列的前項和為
．
（1）求數列的通項公式
及前項和公式；
（2）求數列的通項公式
及前項和公式；
（3）記集合
，若
的子集個數為16，求實數
的取值范圍．
【答案】（1）
（2）
（3）
【解析】
試題（1）數列
是等差數列，可把已知用
表示出來，列出方程組，解出，從而得到通項公式和膠
項和
；（2）由已知得
，這是數列前后項的比值，因此可用連乘法求得通項
，即
，從而有
，它可看作是一個等差數列和一個等比數列的乘積，因此其前項和用乘公比錯位相減法求得；（3）由（1）（2）求得
，不等式
恒成立，即
恒成立，只要求得
的最小值即可，先求出前面幾項
，觀察歸納猜想出
單調性并給出證明（可用
證明數列的單調性），從而可求得最小值，得范圍．
試題解析：（1）設數列
的公差為
，由題意得
（2）由題意得
疊乘得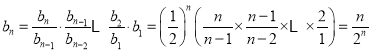
由題意得
①
②
②-①得：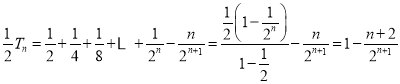
（3）由上面可得令
則
下面研究數列的單調性，
時，
即
單調遞減.
所以不等式
解的個數為4，
.
科目：高中數學 來源： 題型：
【題目】一次猜獎游戲中，1，2，3，4四扇門里擺放了
，
，
，
四件獎品（每扇門里僅放一件）.甲同學說：1號門里是，3號門里是；乙同學說：2號門里是，3號門里是；丙同學說：4號門里是，2號門里是；丁同學說：4號門里是，3號門里是.如果他們每人都猜對了一半，那么4號門里是（ ）
A.B.C.D.
查看答案和解析>>
科目：高中數學 來源： 題型：
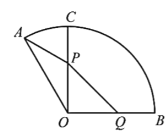
【題目】如圖是一個半徑為1千米的扇形景點的平面示意圖，
.原有觀光道路OC，且
.為便于游客觀賞，景點管理部門決定新建兩條道路PQ、PA，其中P在原道路OC（不含端點O、C）上，Q在景點邊界OB上，且
，同時維修原道路的OP段，因地形原因，新建PQ段、PA段的每千米費用分別是
萬元、
萬元，維修OP段的每千米費用是
萬元.
（1）設
，求所需總費用
，并給出
的取值范圍；
（2）當P距離O處多遠時，總費用最小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司生產的某批產品的銷售量
萬件（生產量與銷售量相等）與促銷費用
萬元滿足
（其中
，
為正常數）．已知生產該產品還需投入成本
萬元（不含促銷費用），產品的銷售價格定為
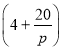元
件．
（1）將該產品的利潤
萬元表示為促銷費用萬元的函數；
（2）促銷費用投入多少萬元時，該公司的利潤最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的兩個焦點
，
與短軸的一個端點構成一個等邊三角形，且直線
與圓
相切.
（1）求橢圓
的方程；
（2）已知過橢圓
的左頂點
的兩條直線
，
分別交橢圓于
，
兩點，且
，求證：直線
過定點，并求出定點坐標；
（3）在（2）的條件下求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2018年遼寧省正式實施高考改革.新高考模式下，學生將根據自己的興趣、愛好、學科特長和高校提供的“選考科目要求”進行選課.這樣學生既能尊重自己愛好、特長做好生涯規劃，又能發揮學科優勢，進而在高考中獲得更好的成績和實現自己的理想.考改實施后，學生將在高二年級將面臨著
的選課模式，其中“3”是指語、數、外三科必學內容，“1”是指在物理和歷史中選擇一科學習，“2”是指在化學、生物、地理、政治四科中任選兩科學習.某校為了更好的了解學生對“1”的選課情況，學校抽取了部分學生對選課意愿進行調查，依據調查結果制作出如下兩個等高堆積條形圖：根據這兩幅圖中的信息，下列哪個統計結論是不正確的（ ）
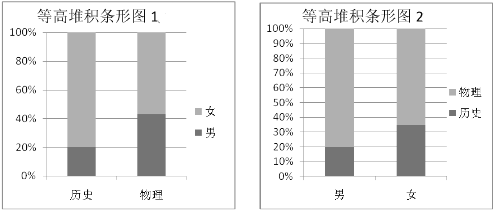
A.樣本中的女生數量多于男生數量
B.樣本中有學物理意愿的學生數量多于有學歷史意愿的學生數量
C.樣本中的男生偏愛物理
D.樣本中的女生偏愛歷史
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的中心在坐標原點，且經過點
，它的一個焦點與拋物線
的焦點重合.
（1）求橢圓的方程；
（2）斜率為
的直線過點
，且與拋物線
交于
兩點，設點
，
的面積為
，求的值；
（3）若直線
過點
，且與橢圓交于
兩點，點
關于
軸的對稱點為
，直線
的縱截距為
，證明：
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
