
【題目】“大眾創(chuàng)業(yè),萬眾創(chuàng)新”是李克強總理在本屆政府工作報告中向全國人民發(fā)出的口號.某生產(chǎn)企業(yè)積極響應號召,大力研發(fā)新產(chǎn)品.為了對新研發(fā)的一批產(chǎn)品進行合理定價,將該產(chǎn)品按事先擬定的價格進行試銷,得到一組銷售數(shù)據(jù)![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知變量![]() ,
, ![]() 具有線性相關關系,求產(chǎn)品銷量
具有線性相關關系,求產(chǎn)品銷量![]() (件)關于試銷單價
(件)關于試銷單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(3)用![]() 表示用正確的線性回歸方程得到的與
表示用正確的線性回歸方程得到的與![]() 對應的產(chǎn)品銷量的估計值.當銷售數(shù)據(jù)
對應的產(chǎn)品銷量的估計值.當銷售數(shù)據(jù)![]() 的殘差的絕對值
的殘差的絕對值![]() 時,則將銷售數(shù)據(jù)
時,則將銷售數(shù)據(jù)![]() 稱為一個“好數(shù)據(jù)”.現(xiàn)從6個銷售數(shù)據(jù)中任取2個,求抽取的2個銷售數(shù)據(jù)中至少有1個是“好數(shù)據(jù)”的概率.
稱為一個“好數(shù)據(jù)”.現(xiàn)從6個銷售數(shù)據(jù)中任取2個,求抽取的2個銷售數(shù)據(jù)中至少有1個是“好數(shù)據(jù)”的概率.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)
;(III)![]() .
.
【解析】試題分析:(1)借助題設條件直接求解;(2)運用相關系數(shù)公式求解;(3)依據(jù)題設條件及新定義的概念和概率公式求解:
試題解析:
解:(Ⅰ) ![]() ,可求得
,可求得![]() .
.
(Ⅱ)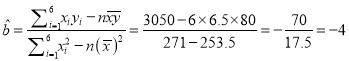 ,
,
![]() ,
,
所以所求的線性回歸方程為![]() .
.
(Ⅲ)當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
與銷售數(shù)據(jù)對比可知滿足![]() (
(![]() 1,2,…,6)的共有3個“好數(shù)據(jù)”:
1,2,…,6)的共有3個“好數(shù)據(jù)”: ![]() 、
、![]() 、
、![]() .
.
從6個銷售數(shù)據(jù)中任意抽取2個的所有可能結(jié)果有![]() 種,
種,
其中2個數(shù)據(jù)中至少有一個是“好數(shù)據(jù)”的結(jié)果有![]() 種,
種,
于是從抽得2個數(shù)據(jù)中至少有一個銷售數(shù)據(jù)中的產(chǎn)品銷量不超過80的概率為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在正四棱錐![]() 中,
中, ![]() 分別是
分別是![]()
的中點,動點![]() 在線段
在線段![]() 上運動時,下列結(jié)論中不恒成立的是( )
上運動時,下列結(jié)論中不恒成立的是( )

A. ![]() 與
與![]() 異面 B.
異面 B. ![]() ∥面
∥面![]()
C. ![]() ⊥
⊥![]() D.
D. ![]() ∥
∥![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在正方形ABCD中,AB=2,點E、F分別在邊AB、DC上,M為AD的中點,且 ![]() =0,則△MEF的面積的取值范圍為( )
=0,則△MEF的面積的取值范圍為( ) 
A.![]()
B.[1,2]
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】黃種人群中各種血型的人所占的比例如下:
血型 | A | B | AB | O |
該血型的人所占比例(%) | 28 | 29 | 8 | 35 |
已知同種血型的人可以輸血,O型血可以輸給任何一種血型的人,其他不同血型的人不能互相輸血,小明是B型血,若小明因病需要輸血,問:
(1)任找一個人,其血可以輸給小明的概率是多少?
(2)任找一個人,其血不能輸給小明的概率是多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某車間共有![]() 名工人,隨機抽取6名,他們某日加工零件個數(shù)的莖葉圖如圖所示,其中莖為十位數(shù),葉為個位數(shù).
名工人,隨機抽取6名,他們某日加工零件個數(shù)的莖葉圖如圖所示,其中莖為十位數(shù),葉為個位數(shù).
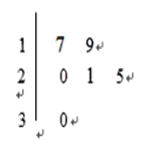
(Ⅰ) 根據(jù)莖葉圖計算樣本均值;
(Ⅱ) 日加工零件個數(shù)大于樣本均值的工人為優(yōu)秀工人,根據(jù)莖葉圖推斷該車間![]() 名工人中有幾名優(yōu)秀工人;
名工人中有幾名優(yōu)秀工人;
(Ⅲ) 從該車間![]() 名工人中,任取2人,求恰有1名優(yōu)秀工人的概率.
名工人中,任取2人,求恰有1名優(yōu)秀工人的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 且
且![]() 為常數(shù)).
為常數(shù)).
(1)當![]() 時,討論函數(shù)
時,討論函數(shù)![]() 在
在![]() 的單調(diào)性;
的單調(diào)性;
(2)設![]() 可求導數(shù),且它的導函數(shù)
可求導數(shù),且它的導函數(shù)![]() 仍可求導數(shù),則
仍可求導數(shù),則![]() 再次求導所得函數(shù)稱為原函數(shù)
再次求導所得函數(shù)稱為原函數(shù)![]() 的二階函數(shù),記為
的二階函數(shù),記為![]() ,利用二階導函數(shù)可以判斷一個函數(shù)的凹凸性.一個二階可導的函數(shù)在區(qū)間
,利用二階導函數(shù)可以判斷一個函數(shù)的凹凸性.一個二階可導的函數(shù)在區(qū)間![]() 上是凸函數(shù)的充要條件是這個函數(shù)在
上是凸函數(shù)的充要條件是這個函數(shù)在![]() 的二階導函數(shù)非負.
的二階導函數(shù)非負.
若![]() 在
在![]() 不是凸函數(shù),求
不是凸函數(shù),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知f(x)=sin2(π+x)﹣cos(2π﹣x)+a
(1)求f(x)的值域
(2)若f(x)在(0, ![]() )內(nèi)有零點,求a的范圍.
)內(nèi)有零點,求a的范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com