
【題目】某港口![]() 要將一件重要物品用小艇送到一艘正在航行的輪船上.在小艇出發時,輪船位于港口
要將一件重要物品用小艇送到一艘正在航行的輪船上.在小艇出發時,輪船位于港口![]() 北偏西
北偏西![]() 且與該港口相距20海里的
且與該港口相距20海里的![]() 處,并以30海里/時的航行速度沿正東方向勻速行駛,假設該小船沿直線方向以
處,并以30海里/時的航行速度沿正東方向勻速行駛,假設該小船沿直線方向以![]() 海里/時的航行速度勻速行駛,經過
海里/時的航行速度勻速行駛,經過![]() 小時與輪船相遇.
小時與輪船相遇.
(1)若希望相遇時小艇的航行距離最小,則小艇航行速度的大小應為多少?
(2)假設小艇的最高航行速度只能達到30海里/時,試設計航行方案(即確定航行方向與航行速度的大小),使得小艇能以最短時間與輪船相遇,并說明理由.
【答案】(1)當t=![]() 時,Smin=10
時,Smin=10![]() ,此時v=
,此時v=![]() =30
=30![]()
(2)航行方向為北偏東30°,航行速度為30海里/小時,小艇能以最短時間與輪船相遇.
【解析】試題分析:(1)設相遇時小艇的航行距離為![]() 海里,則由余弦定理得
海里,則由余弦定理得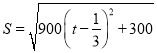 ,再由二次函數的性質求得最值;(2)根據題意,要用時最小,則首先速度最高,即為
,再由二次函數的性質求得最值;(2)根據題意,要用時最小,則首先速度最高,即為![]() 海里/小時,然后是距離最短,則
海里/小時,然后是距離最短,則![]() ,解得
,解得![]() ,再解得相應角.
,再解得相應角.
試題解析:(1)設相遇時小艇的航行距離為![]() 海里,
海里,
則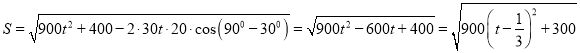
故當![]() 時,
時, 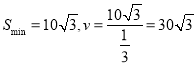
即小艇以![]() 海里/小時的速度航行,相遇小艇的航行距離最小
海里/小時的速度航行,相遇小艇的航行距離最小
(2)
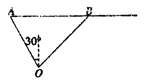
設小艇與輪船在![]() 處相遇.
處相遇.
則![]() ,
,
故![]()
∵![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]()
又![]() 時,
時, ![]() ,
,
故![]() 時,
時, ![]() 取得最小值,且最小值等于
取得最小值,且最小值等于![]()
此時,在![]() 中,有
中,有![]() ,
,
故可設計航行方案如下:
航行方向為北偏東30°,航行速度為30海里/小時


科目:高中數學 來源: 題型:
【題目】某學校1800名學生在一次百米測試中,成績全部介于13秒與18秒之間,抽取其中50個樣本,將測試結果按如下方式分成五組:第一組![]() ,第二組
,第二組![]() ,第五組
,第五組![]() ,下圖是按上述分組方法得到的頻率分布直方圖.
,下圖是按上述分組方法得到的頻率分布直方圖.
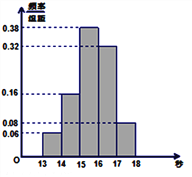
(1)若成績小于15秒認為良好,求該樣本在這次百米測試中成績良好的人數;
(2)請估計學校1800名學生中,成績屬于第四組的人數;
(3)請根據頻率分布直方圖,求樣本數據的眾數、中位數、平均數和方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,公園有一塊邊長為![]() 的等邊
的等邊![]() 的邊角地,現修成草坪,圖中
的邊角地,現修成草坪,圖中![]() 把草坪分成面積相等的兩部分,
把草坪分成面積相等的兩部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.

(1)設![]() (
(![]() ),
),![]() ,求用
,求用![]() 表示
表示![]() 的函數關系式;
的函數關系式;
(2)如果![]() 是灌溉水管,為節約成本,希望它最短,
是灌溉水管,為節約成本,希望它最短,![]() 的位置應在哪里?如果
的位置應在哪里?如果![]() 是參觀線路,則希望它最長,
是參觀線路,則希望它最長,![]() 的位置又應在哪里?請說明理由.
的位置又應在哪里?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高二(1)班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如下,且將全班25人的成績記為![]() 由右邊的程序運行后,輸出
由右邊的程序運行后,輸出![]() .據此解答如下問題:
.據此解答如下問題:
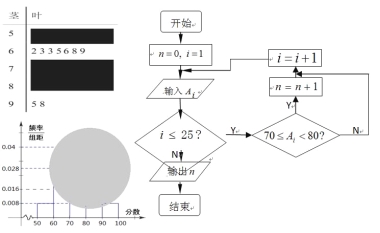
(Ⅰ)求莖葉圖中破損處分數在[50,60),[70,80),[80,90)各區間段的頻數;
(Ⅱ)利用頻率分布直方圖估計該班的數學測試成績的眾數,中位數分別是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中, 以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系, 已知點
軸的非負半軸為極軸建立極坐標系, 已知點![]() 的極坐標為
的極坐標為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() 為參數).
為參數).
(1)直線![]() 過
過![]() 且與曲線
且與曲線![]() 相切, 求直線
相切, 求直線![]() 的極坐標方程;
的極坐標方程;
(2)點![]() 與點
與點![]() 關于
關于![]() 軸對稱, 求曲線
軸對稱, 求曲線![]() 上的點到點
上的點到點![]() 的距離的取值范圍.
的距離的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過研究學生的學習行為,心理學家發現,學生接受能力依賴于老師引入概念和描述問題所用的時間,講座開始時,學生的興趣激增,中間有一段不太長的時間,學生的興趣保持理想的狀態,隨后學生的注意力開始分散,分析結果和實驗表明,用![]() 表示學生掌握和接受概念的能力(
表示學生掌握和接受概念的能力(![]() 的值越大,表示接受能力越強),
的值越大,表示接受能力越強),![]() 表示提出和講授概念的時間(單位:分),可以有以下公式:
表示提出和講授概念的時間(單位:分),可以有以下公式: 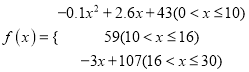 .
.
(1)開講多少分鐘后,學生的接受能力最強?能維持多少分鐘?
(2)開講5分鐘與開講20分鐘比較,學生的接受能力何時強一些?
(3)一個數學難題,需要55的接受能力以及13分鐘的時間,老師能否及時在學生一直達到所需接受能力的狀態下講授完這個難題?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(A)已知![]() ,
, ![]() ,
, ![]() ,且函數
,且函數![]() 的最小正周期為
的最小正周期為![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的值.
的值.
(B)已知![]() ,
, ![]() ,
, ![]() ,且函數
,且函數![]() 的最小正周期為
的最小正周期為![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若關于![]() 的方程
的方程![]() ,在
,在![]() 內有兩個不同的解
內有兩個不同的解![]() ,
, ![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 中,
中,![]() ,且對任意的
,且對任意的![]() 成等比數列,其公比為
成等比數列,其公比為![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若對任意的![]() 成等差數列,其公差為
成等差數列,其公差為![]() .設
.設![]() .
.
①求證:![]() 成等差數列并指出其公差;
成等差數列并指出其公差;
②若![]() ,試求數列
,試求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com