
【題目】如圖,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,過左焦點
,過左焦點![]() 且斜率為
且斜率為![]() 的直線交橢圓
的直線交橢圓![]() 于
于![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() :
:![]() 交橢圓
交橢圓![]() 于
于![]() 兩點.
兩點.

(1)求橢圓![]() 的方程;
的方程;
(2)求證:點![]() 在直線
在直線![]() 上;
上;
(3)是否存在實數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
【答案】(1)![]() (2)詳見解析(3)存在,且
(2)詳見解析(3)存在,且![]()
【解析】
(1)根據離心率和焦點坐標列方程組,解方程組求得![]() 的值,進而求得橢圓
的值,進而求得橢圓![]() 的方程.(2)寫出直線
的方程.(2)寫出直線![]() 的方程,聯立直線的方程和橢圓的方程,求得中點
的方程,聯立直線的方程和橢圓的方程,求得中點![]() 的坐標,將坐標代入直線
的坐標,將坐標代入直線![]() 的方程,滿足方程,由此證得點
的方程,滿足方程,由此證得點![]() 在直線
在直線![]() 上.(3)由(2)知
上.(3)由(2)知![]() 到
到![]() 的距離相等,根據兩個三角形面積的關系,得到
的距離相等,根據兩個三角形面積的關系,得到![]() 是
是![]() 的中點,設出
的中點,設出![]() 點的坐標,聯立直線
點的坐標,聯立直線![]() 的方程和橢圓的方程,求得
的方程和橢圓的方程,求得![]() 點的坐標,并由此求得
點的坐標,并由此求得![]() 的值.
的值.
解:(1) 解:由 ,解得
,解得![]() ,
,![]()
所以所求橢圓的標準方程為![]()
(2)設![]() ,
,![]() ,
,![]() ,
,
![]() ,消
,消![]() 得,
得,![]() ,
,
解得
將![]() 代入到
代入到![]() 中,滿足方程
中,滿足方程
所以點![]() 在直線
在直線![]() 上.
上.
(3)由(2)知![]() 到
到![]() 的距離相等,
的距離相等,
若![]() 的面積是
的面積是![]() 面積的3倍,得
面積的3倍,得![]() ,
,
有![]() ,
,
∴![]() 是
是![]() 的中點,
的中點,
設![]() ,則
,則![]() ,
,
聯立![]() ,解得
,解得![]() ,
,
于是![]()
解得![]() ,所以
,所以![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某市一次全市高中男生身高統計調查數據顯示:全市![]() 名男生的身高服從正態分布
名男生的身高服從正態分布![]() .現從某學校高三年級男生中隨機抽取
.現從某學校高三年級男生中隨機抽取![]() 名測量身高,測量發現被測學生身高全部介于
名測量身高,測量發現被測學生身高全部介于![]() 和
和![]() 之間,將測量結果按如下方式分組:
之間,將測量結果按如下方式分組: ![]() ,
, ![]() ,…,
,…, ![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.

(Ⅰ)試評估該校高三年級男生在全市高中男生中的平均身高狀況;
(Ⅱ)求這![]() 名男生身高在
名男生身高在![]() 以上(含
以上(含![]() )的人數;
)的人數;
(Ⅲ)在這![]() 名男生身高在
名男生身高在![]() 以上(含
以上(含![]() )的人中任意抽取
)的人中任意抽取![]() 人,該
人,該![]() 人中身高排名(從高到低)在全市前
人中身高排名(從高到低)在全市前![]() 名的人數記力
名的人數記力![]() ,求
,求![]() 的數學期望.
的數學期望.
參考數據:若![]() ,則
,則![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 的定義域為
的定義域為![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 的定義域為
的定義域為![]() ,且滿足如下兩個條件:①
,且滿足如下兩個條件:①![]() 在
在![]() 內是單調遞增函數;②存在
內是單調遞增函數;②存在![]() ,使得
,使得![]() 在
在![]() 上的值域為
上的值域為![]() ,那么就稱函數
,那么就稱函數![]() 為“希望函數”,若函數
為“希望函數”,若函數![]() 是“希望函數”,求實數
是“希望函數”,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“龜兔賽跑”講述了這樣的故事:領先的兔子看著慢慢爬行的烏龜,驕傲起來,睡了一覺,當它醒來時,發現烏龜快到終點了,于是急忙追趕,但為時已晚,烏龜還是先到達了終點.用![]() ,
,![]() 分別表示烏龜和兔子所行的路程,
分別表示烏龜和兔子所行的路程,![]() 為時間,則與故事情節相吻合的是( )
為時間,則與故事情節相吻合的是( )
A.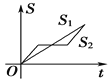 B.
B.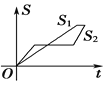 C.
C.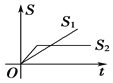 D.
D.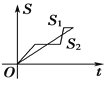
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司決定對旗下的某商品進行一次評估,該商品原來每件售價為25元,年銷售8萬件.
(1)據市場調查,若價格每提高1元,銷售量將相應減少2000件,要使銷售的總收入不低于原收入,該商品每件定價最多為多少元?
(2)為了抓住2022年冬奧會契機,擴大該商品的影響力,提高年銷售量.公司決定立即對該商品進行全面技術革新和銷售策略改革,并提高定價到![]() 元.公司擬投入
元.公司擬投入![]() 萬作為技改費用,投入50萬元作為固定宣傳費用,投入
萬作為技改費用,投入50萬元作為固定宣傳費用,投入![]() 萬元作為浮動宣傳費用.試問:當該商品改革后的銷售量
萬元作為浮動宣傳費用.試問:當該商品改革后的銷售量![]() 至少達到多少萬件時,才可能使改革后的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
至少達到多少萬件時,才可能使改革后的銷售收入不低于原收入與總投入之和?并求出此時商品的每件定價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題![]() 函數
函數![]() 在
在![]() 上單調遞減;命題
上單調遞減;命題![]() 曲線
曲線![]() 為雙曲線.
為雙曲線.
(Ⅰ)若“![]() 且
且![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若“![]() 或
或![]() ”為真命題,“
”為真命題,“![]() 且
且![]() ”為假命題,求實數
”為假命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com