【題目】已知函數
， 
．
（Ⅰ）當
時， 
恒成立，求
的取值范圍；
（Ⅱ）當
時，研究函數
的零點個數；
（Ⅲ）求證： 
(參考數據： 
)．
【答案】(Ⅰ) 
; (Ⅱ)當
時無零點；當
時有一個公共點. (Ⅲ)見解析.
【解析】【試題分析】（1）構造函數借助導數知識運用分類整合思想分析探求；（2）構造函數運用導數知識研究函數的圖像變化情況，確定函數的圖像的交點的個數；（3）借助（1）、（2）的結論運用縮放的方法進行分析推證：
(Ⅰ)令
則
①若
，則
， 
， 
在
遞增， 
，即
在 
恒成立，滿足，所以
；
②若
， 
在
遞增， 
且
且
時， 
，則
使
進而
在
遞減，在
遞增，
所以當
時
，即當
時， 
，不滿足題意，舍去；
綜合①，②知
的取值范圍為
.
(Ⅱ)依題意得
，則
，
則
在
上恒成立，故
在
遞增，
所以
，且
時， 
；
若
，即
，則
，故
在
遞減，所以
，
在
無零點；②若
，即
，則
使
，進而
在
遞減，在
遞增， 
且
時， 
， 
在
上有一個零點，在
無零點，故
在
有一個零點.
綜合①②，當
時無零點；當
時有一個公共點.
(Ⅲ)由(Ⅰ)知，當
時， 
對
恒成立，
令
，則
即
；
由(Ⅱ)知，當
時， 
對
恒成立，
令
，則
，所以
；
故有
.
寒假天地重慶出版社系列答案科目：高中數學 來源： 題型：
【題目】從某校高三上學期期末數學考試成績中，隨機抽取了
名學生的成績得到如圖所示的頻率分布直方圖：
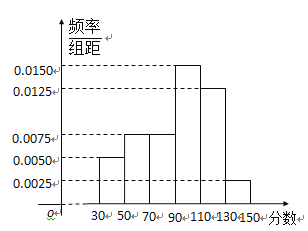
（1）根據頻率分布直方圖，估計該校高三學生本次數學考試的平均分；
（2）若用分層抽樣的方法從分數在
和
的學生中共抽取
人，該人中成績在的有幾人？
（3）在（2）中抽取的人中，隨機抽取
人，求分數在和各
人的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
底面
，底面是直角梯形，
，
，
，
是
上的點．
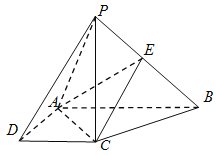
（Ⅰ）求證：平面
⊥平面
；
（Ⅱ）若
是
的中點，且二面角
的余弦值為
，求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲乙丙丁四個物體同時從某一點出發向同一個方向運動，其路程fi（x）（i=1，2，3，4）關于時間x（x≥0）的函數關系式分別為 
， 有以下結論：
①當x＞1時，甲在最前面；
②當x＞1時，乙在最前面；
③當0＜x＜1時，丁在最前面，當x＞1時，丁在最后面；
④丙不可能在最前面，也不可能最最后面；
⑤如果它們已知運動下去，最終在最前面的是甲．
其中，正確結論的序號為（把正確結論的序號都填上，多填或少填均不得分）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
）.
（1）寫出函數
的值域，單調區間（不必證明）；
（2）是否存在實數
使得的定義域為
，值域為
？若存在，求出實數的取值范圍；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一次數學考試中，第22題和第23題為選做題，規定每位考生必須且只須在其中選做一題，現有甲、乙、丙、丁4名考生參加考試，其中甲、乙選做第22題的概率均為
，丙、丁選做第22題的概率均為
．
(Ⅰ)求在甲選做第22題的條件下，恰有兩名考生選做同一道題的概率；
(Ⅱ)設這4名考生中選做第22題的學生個數為X，求X的概率分布及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】東莞市某高級中學在今年4月份安裝了一批空調，關于這批空調的使用年限
（單位：年， 
）和所支出的維護費用
（單位：萬元）廠家提供的統計資料如下：
（1）請根據以上數據，用最小二乘法原理求出維護費用
關于
的線性回歸方程
；
（2）若規定當維護費用
超過13.1萬元時，該批空調必須報廢，試根據（1）的結論求該批空調使用年限的最大值.
參考公式：最小二乘估計線性回歸方程
中系數計算公式：
， 
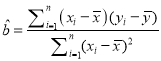查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
