
【題目】給定數列![]() ,若滿足
,若滿足![]() (
(![]() 且
且![]() ),對于任意
),對于任意![]() ,都有
,都有![]() ,則稱數列
,則稱數列![]() 為指數數列.
為指數數列.
(1)已知數列![]() 、
、![]() 的通項公式分別為
的通項公式分別為![]() ,
,![]() ,試判斷
,試判斷![]() 、
、![]() 是不是指數數列(需說明理由);
是不是指數數列(需說明理由);
(2)若數列![]() 滿足:
滿足:![]() ,
,![]() ,
,![]() ,證明:
,證明:![]() 是指數數列;
是指數數列;
(3)若![]() 是指數數列,
是指數數列,![]() ,證明:數列
,證明:數列![]() 中任意三項都不能構成等差數列.
中任意三項都不能構成等差數列.
【答案】(1)![]() 不是指數數列,
不是指數數列,![]() 是指數數列,見解析;(2)見解析;(3)見解析
是指數數列,見解析;(2)見解析;(3)見解析
【解析】
(1)對數列![]() 、
、![]() ,驗證
,驗證![]() 與
與![]() ,
,![]() 與
與![]() 是否相等,由此判斷出
是否相等,由此判斷出![]() 、
、![]() 是不是指數數列.
是不是指數數列.
(2)利用累加法求得數列![]() 的通項公式,然后驗證
的通項公式,然后驗證![]() ,由此證得
,由此證得![]() 是指數數列.
是指數數列.
(3)首先根據指數數列的定義求得數列![]() 的通項公式,利用反證法,證得數列
的通項公式,利用反證法,證得數列![]() 中任意三項都不能構成等差數列.
中任意三項都不能構成等差數列.
(1)對于數列![]() ,
,![]() ,
,![]() ,
,![]() ,因為
,因為![]() ,所以
,所以![]() 不是指數數列.
不是指數數列.
對于數列![]() ,對任意
,對任意![]() ,因為
,因為![]() ,所以
,所以![]() 是指數數列.
是指數數列.
(2)由題意,![]() ,所以數列
,所以數列![]() 是首項為
是首項為![]() ,公比為2的等比數列.所以
,公比為2的等比數列.所以![]() .
.
所以,![]()
![]() ,
,
即![]() 的通項公式為
的通項公式為![]() .所以
.所以![]() ,故
,故![]() 是指數數列.
是指數數列.
(3)因為數列![]() 是指數數列,故對于任意的
是指數數列,故對于任意的![]() ,有
,有![]() ,令
,令![]() ,則
,則![]() ,
,
所以![]() 是首項為
是首項為![]() ,公比為
,公比為![]() 的等比數列,所以,
的等比數列,所以,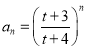 .
.
假設數列![]() 中存在三項
中存在三項![]() ,
,![]() ,
,![]() 構成等差數列,不妨設
構成等差數列,不妨設![]() ,
,
則由![]() ,得
,得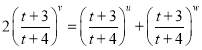 ,所以
,所以![]() ,
,
當![]() 為偶數時,
為偶數時,![]() 是偶數,而
是偶數,而![]() 是偶數,
是偶數,![]() 是奇數,
是奇數,
故![]() 不能成立;
不能成立;
當![]() 為奇數時,
為奇數時,![]() 是偶數,而
是偶數,而![]() 是奇數,
是奇數,![]() 是偶數,
是偶數,
故![]() 也不能成立.
也不能成立.
所以,對任意![]() ,
,![]() 不能成立,
不能成立,
即數列![]() 的任意三項都不成構成等差數列.
的任意三項都不成構成等差數列.
(另證:因為對任意![]() ,
,![]() 一定是偶數,而
一定是偶數,而![]() 與
與![]() 為一奇一偶,故
為一奇一偶,故![]() 與
與![]() 也為一奇一偶,故等式右邊一定是奇數,等式不能成立.)
也為一奇一偶,故等式右邊一定是奇數,等式不能成立.)


科目:高中數學 來源: 題型:
【題目】青島二中高一高二高三三個年級數學MT的學生人數分別為240人,240人,120人,現采用分層抽樣的方法從中抽取5名同學參加團隊內部舉辦的趣味數學比賽,再從5位同學中選出2名一等獎記A=“兩名一等獎來自同一年級”,則事件A的概率為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關命題的說法正確的是__________________.
①命題“若x2-3x+2=0,則x=1”的逆否命題為:若x≠1,則x2-3x+2≠0
②x=1是x2-3x+2=0的充分不必要條件
③若p∧q為假命題,則p,q均為假命題
④對于命題p:x∈R,使得x2+x+1<0,則非p:x∈R, 均有x2+x+1≥0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,正確的是( )
A.一條直線與兩個平行平面中的一個平行,則必與另一個平面平行
B.空間中兩條直線要么平行,要么相交
C.空間中任意的三個點都能唯一確定一個平面
D.對于空間中任意兩條直線,總存在平面與這兩條直線都平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據下圖給出的2000年至2016年我國實際利用外資情況,以下結論正確的是

A. 2000年以來我國實際利用外資規模與年份負相關
B. 2010年以來我國實際利用外資規模逐年增加
C. 2008年我國實際利用外資同比增速最大
D. 2010年以來我國實際利用外資同比增速最大
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】焦點在x軸上的橢圓C:![]() 經過點
經過點![]() ,橢圓C的離心率為
,橢圓C的離心率為![]() .
.![]() ,
,![]() 是橢圓的左、右焦點,P為橢圓上任意點.
是橢圓的左、右焦點,P為橢圓上任意點.
(1)求橢圓的標準方程;
(2)若點M為![]() 的中點(O為坐標原點),過M且平行于OP的直線l交橢圓C于A,B兩點,是否存在實數
的中點(O為坐標原點),過M且平行于OP的直線l交橢圓C于A,B兩點,是否存在實數![]() ,使得
,使得![]() ;若存在,請求出
;若存在,請求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解所經銷商品的使用情況,隨機問卷50名使用者,然后根據這50名的問卷評分數據,統計得到如圖所示的頻率布直方圖,其統計數據分組區間為[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
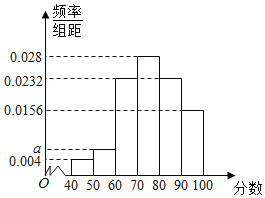
(1)求頻率分布直方圖中a的值;
(2)求這50名問卷評分數據的中位數;
(3)從評分在[40,60)的問卷者中,隨機抽取2人,求此2人評分都在[50,60)的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,焦距為6.
,焦距為6.
(1)求橢圓![]() 的方程.
的方程.
(2)過橢圓左頂點的兩條斜率之積為![]() 的直線分別與橢圓交于
的直線分別與橢圓交于![]() 點.試問直線
點.試問直線![]() 是否過某定點?若過,求出該點的坐標;若不過,請說明理由.
是否過某定點?若過,求出該點的坐標;若不過,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com