
【題目】已知函數![]() ,
,![]() ,m,n
,m,n![]() R.
R.
(1)當m=0時,求函數![]() 的極值;
的極值;
(2)當n=0時,函數![]() 在(0,
在(0,![]() )上為單調函數,求m的取值范圍;
)上為單調函數,求m的取值范圍;
(3)當n>0時,判斷是否存在正數m,使得函數![]() 與
與![]() 有相同的零點,并說明理由.
有相同的零點,并說明理由.
【答案】(1)函數![]() 有極大值﹣1,無極小值;(2)m的取值范圍為{0};(3)存在正數m,使得函數
有極大值﹣1,無極小值;(2)m的取值范圍為{0};(3)存在正數m,使得函數![]() 與
與![]() 有相同的零點,詳見解析.
有相同的零點,詳見解析.
【解析】
(1)當![]() 時,利用
時,利用![]() 研究函數
研究函數![]() 的單調性,由此求得函數
的單調性,由此求得函數![]() 的極值.
的極值.
(2)當![]() 時,由
時,由![]() 或
或![]() 恒成立,將
恒成立,將![]() 分成
分成![]() ,
,![]() ,
,![]() 和
和![]() 四種情況進行分類討論,由此求得
四種情況進行分類討論,由此求得![]() 的取值范圍.
的取值范圍.
(3)設![]() 為相同的零點,由此得到
為相同的零點,由此得到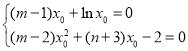 ,進而得到
,進而得到![]() ①,
①,![]() ②.通過構造函數法,結合零點存在性定理,證得①②能同時成立,由此證得存在符合題意的正數
②.通過構造函數法,結合零點存在性定理,證得①②能同時成立,由此證得存在符合題意的正數![]() .
.
(1)當m=0時,![]() ,
,
∴![]() ,令
,令![]() ,解得x=1,列表如下:
,解得x=1,列表如下:
x | (0,1) | 1 | (1, |
| + | 0 | - |
| 單調遞增 | 單調遞減 |
∴當x=1時,函數![]() 有極大值﹣1,無極小值;
有極大值﹣1,無極小值;
(2)當n=0時,函數![]()
∴![]() ,
,
要使函數![]() 在(0,
在(0,![]() )上為單調函數,
)上為單調函數,
則對![]() (0,
(0,![]() ),
),![]() 或
或![]() 恒成立,
恒成立,
令![]() ,
,![]() 或
或![]() 恒成立
恒成立
①當0<m<2時,![]() (0,
(0,![]() )
)![]() (
(![]() ,
,![]() )時,
)時,![]() ,
,![]() (
(![]() ,
,![]() )時,
)時,![]() ,不符題意;
,不符題意;
②當m<0時,![]() (0,
(0,![]() )
)![]() (
(![]() ,
,![]() )時,
)時,![]() ,
,![]() (
(![]() ,
,![]() )時,
)時,![]() ,不符題意;
,不符題意;
③當m≥2時,![]() (0,
(0,![]() )時,
)時,![]() ,
,![]() (
(![]() ,
,![]() )時,
)時,![]() ,不符題意;
,不符題意;
④當m=0時,![]() ,此時
,此時![]() 恒成立,
恒成立,
函數![]() 在(0,
在(0,![]() )上單調遞減,符合題意,
)上單調遞減,符合題意,
綜上所述,m的取值范圍為{0};
(3)∵函數![]() 與
與![]() 有相同的零點,不妨設
有相同的零點,不妨設![]() 為相同的零點
為相同的零點
則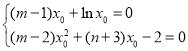 ,
,
得![]() ①,
①,![]() ②,
②,
由(1)知![]() ,故
,故![]() ,
,
∴![]() ,
,
令![]() ,
,
又![]() ,
,![]() ,
,
故當![]() (1,n+3)時,
(1,n+3)時,![]() ,②式有解,且能滿足
,②式有解,且能滿足![]() ,
,
∴存在正數m,使得函數![]() 與
與![]() 有相同的零點.
有相同的零點.


科目:高中數學 來源: 題型:
【題目】(本小題滿分12分,(1)小問7分,(2)小問5分)
設函數![]()
(1)若![]() 在
在![]() 處取得極值,確定
處取得極值,確定![]() 的值,并求此時曲線
的值,并求此時曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若![]() 在
在![]() 上為減函數,求
上為減函數,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科研小組為了研究一種治療新冠肺炎患者的新藥的效果,選50名患者服藥一段時間后,記錄了這些患者的生理指標![]() 和
和![]() 的數據,并統計得到如下的
的數據,并統計得到如下的![]() 列聯表(不完整):
列聯表(不完整):
|
| 合計 | |
| 12 | 36 | |
| 7 | ||
合計 |
其中在生理指標![]() 的人中,設
的人中,設![]() 組為生理指標
組為生理指標![]() 的人,
的人,![]() 組為生理指標
組為生理指標![]() 的人,他們服用這種藥物后的康復時間(單位:天)記錄如下:
的人,他們服用這種藥物后的康復時間(單位:天)記錄如下:
![]() 組:10,11,12,13,14,15,16
組:10,11,12,13,14,15,16
![]() 組:12,13,15,16,17,14,25
組:12,13,15,16,17,14,25
(Ⅰ)填寫上表,并判斷是否有95%的把握認為患者的兩項生理指標![]() 和
和![]() 有關系;
有關系;
(Ⅱ)從![]() ,
,![]() 兩組隨機各選1人,
兩組隨機各選1人,![]() 組選出的人記為甲,
組選出的人記為甲,![]() 組選出的人記為乙,求甲的康復時間比乙的康復時間長的概率.
組選出的人記為乙,求甲的康復時間比乙的康復時間長的概率.
附: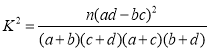 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“垛積術”是我國古代數學的重要成就之一.南宋數學家楊輝在《詳解九章算法》中記載了“方垛”的計算方法:“果子以垛,下方十四個,問計幾何?術曰:下方加一,乘下方為平積.又加半為高,以乘下方為高積.如三而一.”意思是說,將果子以方垛的形式擺放(方垛即每層均為正方形,自下而上每層每邊果子數依次遞減1個,最上層為1個),最下層每邊果子數為14個,問共有多少個果子?計算方法用算式表示為![]() .利用“方垛”的計算方法,可計算最下層每邊果子數為14個的“三角垛”(三角垛即每層均為正三角形,自下而上每層每邊果子數依次遞減1個,最上層為1個)共有果子數為( )
.利用“方垛”的計算方法,可計算最下層每邊果子數為14個的“三角垛”(三角垛即每層均為正三角形,自下而上每層每邊果子數依次遞減1個,最上層為1個)共有果子數為( )
A.420個B.560個C.680個D.1015個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,AB是圓O:x2+y2=1的直徑,且點A在第一象限;圓O1:(x﹣a)2+y2=r2(a>0)與圓O外離,線段AO1與圓O1交于點M,線段BM與圓O交于點N,且![]() ,則a的取值范圍為_______.
,則a的取值范圍為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于圓周率,數學發展史上出現過許多很有創意的求法,如著名的浦豐實驗和查理斯實驗.受其啟發,我們也可以通過設計下面的實驗來估計π的值:先請120名同學每人隨機寫下一個都小于1的正實數對(x,y)且x+y>1;再統計兩數能與1構成鈍角三角形三邊的數對(x,y)的個數m,最后再根據統計數m估計π的值,假如統計結果是m=72,那么可以估計π的值約為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學與文學之間存在著奇妙的聯系,詩中有回文詩,如“山東落花生花落東山,西湖回游魚游回湖西”,倒過來讀,仍然是原句!數學上也有這樣一類數,如66,202,3773,34543,無論從左往右讀,還是從右往左讀,都是同一個數,我們稱這樣的數為“回文數”,現用數字1,2,3,4組數(可重復用),則組成的五位“回文數”的個數為( )
A.24B.28C.48D.64
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() 的準線經過點
的準線經過點![]() ,過
,過![]() 的焦點
的焦點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,
,![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,則下列結論正確的是( )
兩點,則下列結論正確的是( )
A.![]() B.
B.![]() 的最小值為16
的最小值為16
C.四邊形![]() 的面積的最小值為64D.若直線
的面積的最小值為64D.若直線![]() 的斜率為2,則
的斜率為2,則![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com