【題目】為了了解運動健身減肥的效果，某健身房調查了20名肥胖者，健身之前他們的體重(單位：
)情況如柱形圖1所示，經過四個月的健身后，他們的體重情況如柱形圖2所示.對比健身前后，關于這20名肥胖者，下面結論正確的是（ ）
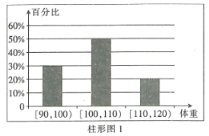
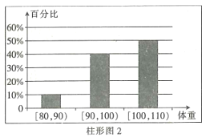
A.他們健身后，體重在區間
內的人數增加了2個
B.他們健身后，體重在區間
內的人數沒有改變
C.因為體重在內所占比例沒有發生變化，所以說明健身對體重沒有任何影響
D.他們健身后，原來體重在區間
內的肥胖者體重都有減少
科目：高中數學 來源： 題型：
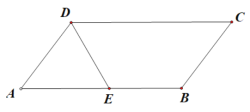
【題目】如圖，已知平行四邊形
中，
，
，
為邊
的中點，將
沿直線
翻折成
.若
為線段
的中點.
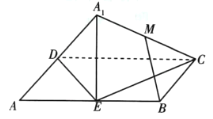
（1）證明
平面
，并求
的長；
（2）在翻折過程中，當三棱錐
的體積取最大時，求平面
與平面所成的二面角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國在歐洲的某孔子學院為了讓更多的人了解中國傳統文化，在當地舉辦了一場由當地人參加的中國傳統文化知識大賽，為了了解參加本次大賽參賽人員的成績情況，從參賽的人員中隨機抽取
名人員的成績（滿分100分）作為樣本，將所得數據進行分析整理后畫出頻率分布直方圖如圖所示，已知抽取的人員中成績在[50，60）內的頻數為3.
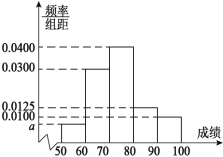
（1）求的值和估計參賽人員的平均成績（保留小數點后兩位有效數字）；
（2）已知抽取的名參賽人員中，成績在[80，90）和[90，100]女士人數都為2人，現從成績在[80，90）和[90，100]的抽取的人員中各隨機抽取2人，記這4人中女士的人數為
，求的分布列與數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
（其中
，點P的軌跡記為曲線
，以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，點Q在曲線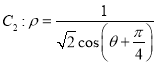
上．
（1）求曲線的極坐標方程和曲線
的直角坐標方程；
（2）當
，
時，求曲線與曲線的公共點的極坐標
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
：
的離心率
，其左焦點
到此雙曲線漸近線的距離為
.
（1）求雙曲線的方程；
（2）若過點
的直線
交雙曲線于
兩點，且以為直徑的圓
過原點
，求圓的圓心到拋物線
的準線的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某外賣平臺為提高外賣配送效率，針對外賣配送業務提出了兩種新的配送方案，為比較兩種配送方案的效率，共選取50名外賣騎手，并將他們隨機分成兩組，每組25人，第一組騎手用甲配送方案，第二組騎手用乙配送方案.根據騎手在相同時間內完成配送訂單的數量（單位：單）繪制了如下莖葉圖：
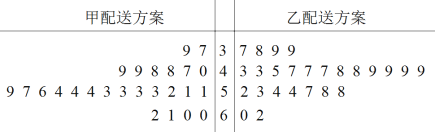
（1）根據莖葉圖，求各組內25位騎手完成訂單數的中位數，已知用甲配送方案的25位騎手完成訂單數的平均數為52，結合中位數與平均數判斷哪種配送方案的效率更高，并說明理由；
（2）設所有50名騎手在相同時間內完成訂單數的平均數
，將完成訂單數超過記為“優秀”，不超過記為“一般”，然后將騎手的對應人數填入下面列聯表；
優秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
（3）根據（2）中的列聯表，判斷能否有
的把握認為兩種配送方案的效率有差異.
附：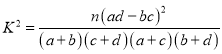
，其中
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
由方程
確定，對于函數
給出下列命題：
①存在
，
，使得
成立；
②
，
，使得
且
同時成立；
③對于任意
，
恒成立；
④對任意，，
；都有
恒成立．
其中正確的命題共有（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】國慶70周年閱兵式上的女兵們是一道靚麗的風景線，每一名女兵都是經過層層篩選才最終入選受閱方隊，篩選標準非常嚴格，例如要求女兵身高（單位：cm）在區間
內.現從全體受閱女兵中隨機抽取200人，對她們的身高進行統計，將所得數據分為
，
，
，
，
五組，得到如圖所示的頻率分布直方圖，其中第三組的頻數為75，最后三組的頻率之和為0.7.
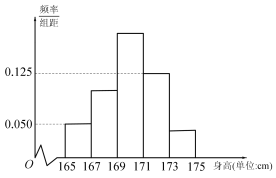
（1）請根據頻率分布直方圖估計樣本的平均數
和方差
（同一組中的數據用該組區間的中點值代表）；
（2）根據樣本數據，可認為受閱女兵的身高X（cm）近似服從正態分布
，其中
近似為樣本平均數，
近似為樣本方差.
（i）求
；
（ii）若從全體受閱女兵中隨機抽取10人，求這10人中至少有1人的身高在174.28cm以上的概率.
參考數據：若
，則
，
，
，
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
的底面為菱形，
，
．平面
平面
，
，
，
分別是
，
的中點．
（1）求證：
//平面
；
（2）若直線
與平面所成的角為
，求直線
與平面
所成角的正弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
