
【題目】已知隨機變量X~N(μ,σ2),且其正態曲線在(-∞,80)上是增函數,在(80,+∞)上為減函數,且P(72≤X≤88)=0.682 6.
(1)求參數μ,σ的值;
(2)求P(64<X≤72).
【答案】(1)μ=80,σ=8 (2)0.135 5
【解析】(1)由于正態曲線在(-∞,80)上是增函數,在(80,+∞)上是減函數,所以正態曲線關于直線x=80對稱,即參數μ=80.
又P(72≤x≤88)=0.682 6,結合P(μ-σ<X<μ+σ)=0.682 6,可知σ=8.
(2)∵P(μ-2σ<X<μ+2σ)=P(64<X<96)=0.954 4.
又∵P(X<64)=P(X>96),
∴P(X<64)=![]() (1-0.954 4)=
(1-0.954 4)=![]() ×0.045 6=0.022 8.
×0.045 6=0.022 8.
∴P(X>64)=0.977 2.
又P(X≤72)=![]() (1-P(72≤X≤88))
(1-P(72≤X≤88))
=![]() (1-0.682 6)=0.158 7,
(1-0.682 6)=0.158 7,
P(64<X≤72)=P(X>64)-P(X>72)
=0.977 2-(1-0.158 7)=0.135 9.


 天天練口算系列答案
天天練口算系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)函數![]() 的圖象與
的圖象與![]() 的圖象無公共點,求實數
的圖象無公共點,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)是否存在實數![]() ,使得對任意的
,使得對任意的![]() ,都有函數
,都有函數![]() 的圖象在
的圖象在![]() 的圖象的下方?若存在,請求出整數
的圖象的下方?若存在,請求出整數![]() 的最大值;若不存在,請說理由.
的最大值;若不存在,請說理由.
(參考數據:![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次籃球定點投籃訓練中,規定每人最多投3次,在![]() 處每投進一球得3分;在
處每投進一球得3分;在![]() 處每投進一球得2分,如果前兩次得分之和超過3分就停止投籃;否則投第3次,某同學在
處每投進一球得2分,如果前兩次得分之和超過3分就停止投籃;否則投第3次,某同學在![]() 處的抽中率
處的抽中率![]() ,在
,在![]() 處的抽中率為
處的抽中率為![]() ,該同學選擇現在
,該同學選擇現在![]() 處投第一球,以后都在
處投第一球,以后都在![]() 處投,且每次投籃都互不影響,用
處投,且每次投籃都互不影響,用![]() 表示該同學投籃訓練結束后所得的總分,其分布列為:
表示該同學投籃訓練結束后所得的總分,其分布列為:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求隨機變量![]() 的數學期望
的數學期望![]() ;
;
(3)試比較該同學選擇上述方式投籃得分超過3分與選擇都在![]() 處投籃得分超過3分的概率的大小.
處投籃得分超過3分的概率的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}中,a2=5,S5=40.等比數列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通項公式
(2)令cn=anbn,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲、乙兩名學生中選拔一人參加射箭比賽,為此需要對他們的射箭水平進行測試.現這兩名學生在相同條件下各射箭10次,命中的環數如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)計算甲、乙兩人射箭命中環數的平均數和標準差;
(2)比較兩個人的成績,然后決定選擇哪名學生參加射箭比賽.
查看答案和解析>>
科目:高中數學 來源: 題型:
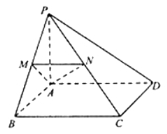
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,點
為正方形,點![]() 分別為線段
分別為線段![]() 上的點,
上的點,![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求證:當點![]() 不與點
不與點![]() 重合時,
重合時,![]() 平面
平面![]() ;
;
(3)當![]() ,
,![]() 時,求點
時,求點![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() , 若
, 若![]() 成等比數列,橢圓
成等比數列,橢圓![]() 上的點到焦點
上的點到焦點![]() 的最短距離為
的最短距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設![]() 為直線
為直線![]() 上任意一點,過
上任意一點,過![]() 的直線交橢圓
的直線交橢圓![]() 于點
于點![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(I)求橢圓![]() 的方程;
的方程;
(II)設動直線![]() 與橢圓
與橢圓![]() 有且僅有一個公共點,判斷是否存在以原點
有且僅有一個公共點,判斷是否存在以原點![]() 為圓心的圓,滿足此圓與
為圓心的圓,滿足此圓與![]() 相交于兩點
相交于兩點![]() (兩點均不在坐標軸上),且使得直線
(兩點均不在坐標軸上),且使得直線![]() 的斜率之積為定值?若存在,求此圓的方程;若不存在,說明理由.
的斜率之積為定值?若存在,求此圓的方程;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com