
【題目】已知函數(shù)![]() ,
,![]() .
.
(Ⅰ)函數(shù)![]() 的圖象與
的圖象與![]() 的圖象無公共點,求實數(shù)
的圖象無公共點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)是否存在實數(shù)![]() ,使得對任意的
,使得對任意的![]() ,都有函數(shù)
,都有函數(shù)![]() 的圖象在
的圖象在![]() 的圖象的下方?若存在,請求出整數(shù)
的圖象的下方?若存在,請求出整數(shù)![]() 的最大值;若不存在,請說理由.
的最大值;若不存在,請說理由.
(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ).
).
【答案】(Ⅰ)![]() ,(Ⅱ)1
,(Ⅱ)1
【解析】
試題分析:(Ⅰ)函數(shù)圖象無公共點,可以轉(zhuǎn)化為方程![]() 無實根,此方程可用分離參數(shù)法化為
無實根,此方程可用分離參數(shù)法化為![]() 無實根,從而只要求出函數(shù)
無實根,從而只要求出函數(shù)![]() 的值域即可,這可導(dǎo)數(shù)的知識求得;(Ⅱ)同樣問題轉(zhuǎn)化為“不等式
的值域即可,這可導(dǎo)數(shù)的知識求得;(Ⅱ)同樣問題轉(zhuǎn)化為“不等式![]() 對
對![]() 恒成立”,即
恒成立”,即![]() 對
對![]() 恒成立,因此問題轉(zhuǎn)化為
恒成立,因此問題轉(zhuǎn)化為
求函數(shù)![]() 的最小值.
的最小值.
試題解析:(Ⅰ)函數(shù)![]() 與
與![]() 無公共點,
無公共點,
等價于方程![]() 在
在![]() 無解
無解
令![]() ,則
,則![]() 令
令![]() 得
得![]()
|
|
|
|
| + | 0 | - |
| 增 | 極大值 | 減 |
因為![]() 是唯一的極大值點,故
是唯一的極大值點,故![]()
故要使方程![]() 在
在![]() 無解,
無解,
當(dāng)且僅當(dāng)![]() ,故實數(shù)
,故實數(shù)![]() 的取值范圍為
的取值范圍為![]()
(Ⅱ)假設(shè)存在實數(shù)![]() 滿足題意,則不等式
滿足題意,則不等式![]() 對
對![]() 恒成立.
恒成立.
即![]() 對
對![]() 恒成立.
恒成立.
令![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() ,
,
∵![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]() ,
,![]() ,
,
且![]() 的圖象在
的圖象在![]() 上連續(xù),
上連續(xù),
∴存在![]() ,使得
,使得![]() ,即
,即![]() ,則
,則![]() ,
,
∴ 當(dāng)![]() 時,
時,![]() 單調(diào)遞減;
單調(diào)遞減;
當(dāng)![]() 時,
時,![]() 單調(diào)遞增,
單調(diào)遞增,
則![]() 取到最小值
取到最小值![]()
 ,
,
∴ ![]() ,即
,即![]() 在區(qū)間
在區(qū)間![]() 內(nèi)單調(diào)遞增.
內(nèi)單調(diào)遞增.
![]() ,
,
∴存在實數(shù)![]() 滿足題意,且最大整數(shù)
滿足題意,且最大整數(shù)![]() 的值為
的值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四棱錐![]() ,底面
,底面![]() 是
是![]() 、邊長為
、邊長為![]() 的菱形,又
的菱形,又![]() 底
底![]() ,且
,且![]() ,點
,點![]() 分別是棱
分別是棱![]() 的中點.
的中點.
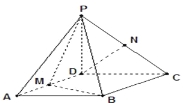
(1)證明:![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求點![]() 到平面
到平面![]() 的距離.[
的距離.[
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() .
.
(1)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線的斜率;
處的切線的斜率;
(2)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間與極值.
的單調(diào)區(qū)間與極值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)有編號分別為1,2,3,4,5的五道不同的政治題和編號分別為6,7,8,9的四道不同的歷史題.甲同學(xué)從這九道題中一次性隨機抽取兩道題,每道題被抽到的概率是相等的,用符號(x,y)表示事件“抽到的兩道題的編號分別為x,y,且x<y.”.
(1)問有多少個基本事件,并列舉出來;
(2)求甲同學(xué)所抽取的兩道題的編號之和小于17但不小于11的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某投資商到一開發(fā)區(qū)投資72萬元建起一座蔬菜加工廠,第一年共支出12萬元,以后每年支出增加4萬元,從第一年起每年的蔬菜銷售收入均為50萬元,設(shè)![]() 表示前
表示前![]() 年的純利潤總和(
年的純利潤總和(![]() =前
=前![]() 年的總收入
年的總收入![]() 前
前![]() 年的總支出
年的總支出![]() 投資額).
投資額).
(1)該廠從第幾年開始盈利?
(2)若干年后,投資商為開發(fā)新項目,對該廠有兩種處理方案:
① 當(dāng)年平均利潤達到最大時,以48萬元出售該廠;
② 當(dāng)純利潤總和達到最大時,以16萬元出售該廠,
問哪種方案更合算?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ax2+bx(a≠0)的導(dǎo)函數(shù)f′(x)=-2x+7,數(shù)列{an}的前n項和為Sn,點Pn(n,Sn)(n∈N*)均在函數(shù)y=f(x)的圖象上,求數(shù)列{an}的通項公式及Sn的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 的對稱軸為
的對稱軸為![]() ,
,![]() .
.
(1)求函數(shù)![]() 的最小值及取得最小值時
的最小值及取得最小值時![]() 的值;
的值;
(2)試確定![]() 的取值范圍,使
的取值范圍,使![]() 至少有一個實根;
至少有一個實根;
(3)當(dāng)![]() 時,
時,![]() ,對任意
,對任意![]() 有
有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知隨機變量X~N(μ,σ2),且其正態(tài)曲線在(-∞,80)上是增函數(shù),在(80,+∞)上為減函數(shù),且P(72≤X≤88)=0.682 6.
(1)求參數(shù)μ,σ的值;
(2)求P(64<X≤72).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com