【題目】已知拋物線
: 
過點
的直線交拋物線于
兩點，設
(1)若點 
關于
軸的對稱點為
，求證：直線
經過拋物線 的焦點
；
(2)若
求當
最大時，直線
的方程．
【答案】(1)證明見解析.
(2)
.
【解析】試題分析：（1）設出P和Q的坐標，根據P和M關于x軸對稱表示出M的坐標，利用設出的坐標表示出
和
，根據
，化簡即可得到P和Q的橫坐標，然后由拋物線的方程找出焦點F的坐標，然后利用M，F(xiàn)和Q的坐標表示出向量
，利用剛才化簡的式子及求出的橫坐標代入即可得到=λ
，所以得到直線MQ過F點；（2）由第一問求得的P和Q的橫坐標相乘等于1，由y12﹣y22=16x1x2=16，y1y2＞0，得到y(tǒng)1y2的值，利用兩點間的距離公式表示出|PQ|2，然后把P和Q的橫坐標及得到的y1y2的值及x1x2的值分別代入得到關于λ的關系式，配方后利用λ的范圍求出λ+
的范圍，即可求出λ+的最大值，讓其等于最大值解出此時λ的值，把λ的值代入關于λ的關系式即可求出|PQ|2的最大值，即得到|PQ|最大值，并利用λ的值求出此時P和Q兩點的坐標，根據兩點的坐標即可寫出直線PQ的方程．
詳解：
（1）設
由拋物線C：
得到F（1，0）
直線MQ經過拋物線C的焦點F；
（2）由（1）知
則
當 
即 
時， 
有最大值
，則
的最大值為
此時
則直線的方程為：
科目：高中數學 來源： 題型：
【題目】（1）在
中，內角
，
，
的對邊分別為
，
，
，且
，證明：
；
（2）已知結論：在直角三角形中，若兩直角邊長分別為，，斜邊長為，則斜邊上的高
.若把該結論推廣到空間：在側棱互相垂直的四面體
中，若三個側面的面積分別為
，
，
，底面面積為
，則該四面體的高
與，，，之間的關系是什么？（用，，，表示）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一次趣味校園運動會的頒獎儀式上,高一、高二、高三代表隊人數分別為120人、120人、n人.為了活躍氣氛,大會組委會在頒獎過程中穿插抽獎活動,并用分層抽樣的方法從三個代表隊中共抽取20人在前排就座,其中高二代表隊有6人.
(1)求n的值;
(2)把在前排就座的高二代表隊6人分別記為a,b,c,d,e,f,現(xiàn)隨機從中抽取2人上臺抽獎.求a和b至少有一人上臺抽獎的概率;
(3)抽獎活動的規(guī)則是:代表通過操作按鍵使電腦自動產生兩個[0,1]之間的均勻隨機數x,y,并按如圖所示的程序框圖執(zhí)行.若電腦顯示“中獎”,則該代表中獎;若電腦顯示“謝謝”,則不中獎,求該代表中獎的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】國慶假期是實施免收小型客車高速通行費的重大節(jié)假日，有一個群名為“天狼星”的自駕游車隊，該車隊是由31輛身長約為
（以
計算）的同一車型組成，行程中經過一個長為2725
的隧道（通過隧道的車速不超過
），勻速通過該隧道，設車隊的速度為
，根據安全和車流的需要，當
時，相鄰兩車之間保持
的距離；當
時，相鄰兩車之間保持
的距離，自第一輛車車頭進入隧道至第31輛車車尾離開隧道所用的時間
．
（1）將
表示成為
的函數；
（2）求該車隊通過隧道時間
的最小值及此時車隊的速度．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合A={x|x2-（a-1）x-a＜0，a∈R}，集合B={x|
＜0}．
（1）當a=3時，求A∩B；
（2）若A∪B=R，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校某次N名學生的學科能力測評成績（滿分120分）的頻率分布直方圖如下，已知分數在100﹣110的學生數有21人
（1）求總人數N和分數在110﹣115分的人數n．；
（2）現(xiàn)準備從分數在110﹣115的n名學生（女生占 
）中選3位分配給A老師進行指導，設隨機變量ξ表示選出的3位學生中女生的人數，求ξ的分布列與數學期望Eξ；
（3）為了分析某個學生的學習狀態(tài)，對其下一階段的學習提供指導建議，對他前7次考試的數學成績x、物理成績y進行分析，該生7次考試成績如表
數學（x） | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理（y） | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知該生的物理成績y與數學成績x是線性相關的，求出y關于x的線性回歸方程 
= 
x+ 
．若該生的數學成績達到130分，請你估計他的物理成績大約是多少？
附：對于一組數據（x1 ， y1），（x2 ， y2），…，（xn ， yn），其回歸方程 = x+ 的斜率和截距的最小二乘估計分別為 = 
， 
．
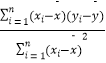查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某小學慶“六一”晚會共由6個節(jié)目組成，演出順序有如下要求：節(jié)目
必須排在前兩位，節(jié)目
不能排在第一位，節(jié)目
必須排在最后一位，該臺晚會節(jié)目演出順序的編排方案共有（ ）
A. 36種 B. 42種 C. 48種 D. 54種
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是公差不為0的等差數列，首項a1=1，且a1 ， a2 ， a4成等比數列． （Ⅰ）求數列{an}的通項公式；
（Ⅱ）設數列{bn}滿足bn=an+2 
，求數列{bn}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x），g（x）的定義域都是D，直線x=x0（x0∈D），與y=f（x），y=g（x）的圖象分別交于A，B兩點，若|AB|的值是不等于0的常數，則稱曲線y=f（x），y=g（x）為“平行曲線”，設f（x）=ex-alnx+c（a>0，c≠0），且y=f（x），y=g（x）為區(qū)間（0，+
）的“平行曲線”，g（1）=e，g（x）在區(qū)間（2，3）上的零點唯一，則a的取值范圍是_________.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com