
【題目】函數(shù)y=﹣sin(ωx+φ)(ω>0,φ∈(﹣ ![]() ,
, ![]() ))的一條對稱軸為x=
))的一條對稱軸為x= ![]() ,一個對稱中心為(
,一個對稱中心為( ![]() ,0),在區(qū)間[0,
,0),在區(qū)間[0, ![]() ]上單調(diào).
]上單調(diào).
(1)求ω,φ的值;
(2)用描點法作出y=sin(ωx+φ)在[0,π]上的圖象.
【答案】
(1)解:由題意得: 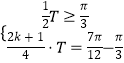 ,即
,即 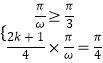 ,解得
,解得 ![]()
又ω>0,k∈Z,所以ω=2,
x= ![]() 為對稱軸,2×
為對稱軸,2× ![]() +φ=kπ+
+φ=kπ+ ![]() ,所以φ=kπ﹣
,所以φ=kπ﹣ ![]() ,
,
又φ∈(﹣ ![]() ,
, ![]() ),
),
∴φ=﹣ ![]()
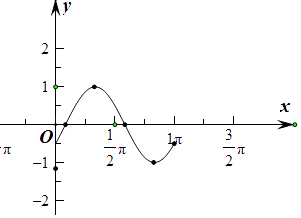
(2)解:由(1)可知f(x)=sin(2x﹣ ![]() ),
),
由x∈[0,π],
所以2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
列表:
2x﹣ | ﹣ | 0 |
| π |
|
|
x | 0 |
|
|
|
| π |
f(x) | ﹣ | 0 | 1 | 0 | ﹣1 |
|
畫圖:
【解析】(1)由條件利用三角形函數(shù)的周期,對稱軸,對稱中心,即可ω,φ.(2)用五點法作函數(shù)y=Asin(ωx+φ)在一個周期[0,π]上的圖象.
【考點精析】解答此題的關鍵在于理解五點法作函數(shù)y=Asin(ωx+φ)的圖象的相關知識,掌握描點法及其特例—五點作圖法(正、余弦曲線),三點二線作圖法(正、余切曲線).


科目:高中數(shù)學 來源: 題型:
【題目】某闖關游戲有這樣一個環(huán)節(jié):該關卡有一道上了鎖的門,要想通過該關卡,要拿到門前密碼箱里的鑰匙,才能開門過關.但是密碼箱需要一個密碼才能打開,并且3次密碼嘗試錯誤,該密碼箱被鎖定,從而闖關失敗.某人到達該關卡時,已經(jīng)找到了可能打開密碼箱的6個密碼(其中只有一個能打開密碼箱),他決定從中隨機地選擇1個密碼進行嘗試.若密碼正確,則通關成功;否則繼續(xù)嘗試,直至密碼箱被鎖定.
(1)求這個人闖關失敗的概率;
(2)設該人嘗試密碼的次數(shù)為X,求X的分布列和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在正方體ABCD-A1B1C1D1中,有下面結(jié)論:

①AC∥平面CB1D1;
②AC1⊥平面CB1D1;
③AC1與底面ABCD所成角的正切值是![]() ;
;
④AD1與BD為異面直線.其中正確的結(jié)論的序號是________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設f(x)= ![]() ,曲線y=f(x)在點(1,f(1))處的切線與直線2x+y+1=0垂直.
,曲線y=f(x)在點(1,f(1))處的切線與直線2x+y+1=0垂直.
(1)求a的值;
(2)若x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖1,在高為2的梯形ABCD中,![]() ,
,![]() ,
,![]() ,過A、B分別作
,過A、B分別作![]() ,
,![]() ,垂足分別為E、
,垂足分別為E、![]() 已知
已知![]() ,將D、C沿AE、BF折向同側(cè),得空間幾何體
,將D、C沿AE、BF折向同側(cè),得空間幾何體![]() ,如圖2.
,如圖2.

![]() 若
若![]() ,求證:
,求證:![]() ;
;
![]() 若
若![]() ,線段AB的中點是P,求CP與平面ACD所成角的正弦值.
,線段AB的中點是P,求CP與平面ACD所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓C:![]() 及點
及點![]() ,
,![]() .
.
![]() 過B作直線l與圓C相交于M,N兩點,
過B作直線l與圓C相交于M,N兩點,![]() ,求直線l的方程;
,求直線l的方程;
![]() 在圓C上是否存在點P,使得
在圓C上是否存在點P,使得![]() ?若存在,求點P的個數(shù);若不存在,說明理由.
?若存在,求點P的個數(shù);若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列函數(shù)中,既是偶函數(shù)又在區(qū)間(0,+∞)上是單調(diào)增函數(shù)的是( )
A.![]()
B.y=|x|﹣1
C.y=lgx
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
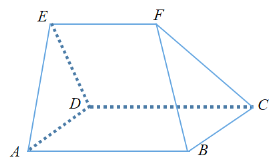
【題目】如圖幾何體![]() 中,等邊三角形
中,等邊三角形![]() 所在平面垂直于矩形
所在平面垂直于矩形![]() 所在平面,又知
所在平面,又知![]() ,
,![]() //
//![]() .
.
(1)若![]() 的中點為
的中點為![]() ,
,![]() 在線段
在線段![]() 上,
上,![]() //平面
//平面![]() ,求
,求![]() ;
;
(2)若平面![]() 與平面
與平面![]() 所成二面角
所成二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角
所成角![]() 的正弦值;
的正弦值;
(3)若![]() 中點為
中點為![]() ,
,![]() ,求
,求![]() 在平面
在平面![]() 上的正投影。
上的正投影。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
(1)求![]() 的方程;
的方程;
(2)若動點![]() 在直線
在直線![]() 上,過
上,過![]() 作直線交橢圓
作直線交橢圓![]() 于
于![]() 兩點,使得
兩點,使得![]() ,再過
,再過![]() 作直線
作直線![]() ,證明:直線
,證明:直線![]() 恒過定點,并求出該定點的坐標.
恒過定點,并求出該定點的坐標.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com