
���}Ŀ����֪���タ![]() ��
��![]()
![]() �����c(di��n)
�����c(di��n)![]() ����������^�c(di��n)
����������^�c(di��n)![]()
![]() ��ֱ��
��ֱ��![]() �c���タ
�c���タ![]() ���ڲ�ͬ�ă��c(di��n)
���ڲ�ͬ�ă��c(di��n)![]() .
.![]() ��ʹ��
��ʹ��![]() ���t�Q�c(di��n)
���t�Q�c(di��n)![]() �钁�タ
�钁�タ![]() ����
����![]() ���c(di��n)����
���c(di��n)����
��1�����![]() ��ֱ��
��ֱ��![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
��2�����![]() �钁�タ
�钁�タ![]() ����
����![]() ���c(di��n)������ֱ��
���c(di��n)������ֱ��![]() �ķ��̣�
�ķ��̣�
��3���C���c(di��n)![]() ���ǒ��タ
���ǒ��タ![]() ����2���c(di��n)����
����2���c(di��n)����
��4�����![]()
![]() �ǒ��タ����2���c(di��n)������
�ǒ��タ����2���c(di��n)������![]() ��ȡֵ������
��ȡֵ������
���𰸡���1��![]() ����2��
����2��![]() ����3���C��Ҋ��������4��
����3���C��Ҋ��������4��![]()
��������
��1��(li��n)��![]() ����c(di��n)
����c(di��n)![]() ,�c(di��n)
,�c(di��n)![]() ������(bi��o),�Ķ��������������e,�M(j��n)�����
������(bi��o),�Ķ��������������e,�M(j��n)�����![]() ��
��
��2����![]() �ɵ�
�ɵ�![]() ,�t
,�t![]() ,(li��n)��ֱ��
,(li��n)��ֱ��![]() ��
��![]() �c���タ,���f�_(d��)�����ɵ�
�c���タ,���f�_(d��)�����ɵ�![]() �c
�c![]() ���P(gu��n)ϵ,�M(j��n)�����
���P(gu��n)ϵ,�M(j��n)�����![]() ,�Ķ��õ�ֱ�����̣�
,�Ķ��õ�ֱ�����̣�
��3�����O(sh��)����,�O(sh��)ֱ��![]() ��
��![]() ,�����c(di��n)��ֱ�����x��ʽ�����e,�����ɵ�
,�����c(di��n)��ֱ�����x��ʽ�����e,�����ɵ�![]() ,��ֱ���c���タ(li��n)���ɵ�
,��ֱ���c���タ(li��n)���ɵ�![]() ,�ʿ��C�����O(sh��)��������
,�ʿ��C�����O(sh��)��������
��4���O(sh��)ֱ��![]() ��
��![]() ,(li��n)��ֱ���c���タ��
,(li��n)��ֱ���c���タ��![]() ,�t����(j��)�f�_(d��)�����ɵ�
,�t����(j��)�f�_(d��)�����ɵ�![]() �c
�c![]() ���P(gu��n)ϵ,��
���P(gu��n)ϵ,��![]() Ҳ���Եõ�
Ҳ���Եõ�![]() �c
�c![]() ���P(gu��n)ϵ,���߽Y(ji��)�Ͽɵ�
���P(gu��n)ϵ,���߽Y(ji��)�Ͽɵ�![]() ,�M(j��n)����⼴��
,�M(j��n)����⼴��
�⣺��1��(li��n)��![]() ��
��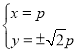 ,�t
,�t![]() ,
,![]() ,
,
����![]() ,
,
![]() ,
,
����![]() ,
,
��![]()
��2���O(sh��)![]() .
.![]() ,�����O(sh��)
,�����O(sh��)![]() ,
,![]() ,�O(sh��)ֱ��
,�O(sh��)ֱ��![]() ��
��![]() ,
,
���![]() ,
,
����![]() ,��
,��![]() ,
,
��![]() ����
����![]() ��
��![]() ,
,
���� ,�t
,�t ,����
,����![]() ��
��
����ֱ��![]() ��
��![]() ,��
,��![]()
��3���O(sh��)ֱ��![]() ��
��![]() ��
��![]() ��,����
��,����![]() ������,
������,![]() ,
,
���f�_(d��)������ ,����
,����![]() ,
,
�t�c(di��n)![]() ��ֱ��
��ֱ��![]() ��
��![]() �ľ��x
�ľ��x![]() ,
,
��![]() ��
��![]() ,���
,���![]() ,
,
��![]() ��
��![]() ��,
��,![]() ,��
,��![]() ��
��![]() ,
,
��![]() ���뻯����
���뻯����![]() ,���
,���![]() ,������,
,������,
�����c(di��n)![]() ���ǒ��タ
���ǒ��タ![]() ����2���c(di��n)����
����2���c(di��n)����
��4���O(sh��)![]() ,
,![]() ,�����O(sh��)
,�����O(sh��)![]() ,
,![]() ,
,
�O(sh��)ֱ��![]() ��
��![]() ,
,
��ֱ��![]() ����
����![]() ��
��![]() ,
,
�t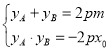 ,
,
��![]() ,��
,��![]() ,���
,���![]() ,
,
���� ,��
,��![]() ��
��![]() ,���
,���![]() ��
��


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ăAб�Ǟ�
�ăAб�Ǟ�![]() ���ҽ�(j��ng)�^�c(di��n)
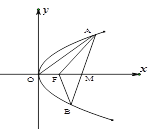
���ҽ�(j��ng)�^�c(di��n)![]() ��������(bi��o)ԭ�c(di��n)O��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ��ֱ��
��������(bi��o)ԭ�c(di��n)O��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ��ֱ��![]() ����ԭ�c(di��n)O���侀��
����ԭ�c(di��n)O���侀��![]() ���c(di��n)M���c(di��n)N���侀OM�ϵ��c(di��n)���M��
���c(di��n)M���c(di��n)N���侀OM�ϵ��c(di��n)���M��![]() ��ӛ�c(di��n)N��܉�E������C��
��ӛ�c(di��n)N��܉�E������C��
�������ֱ��![]() �ą���(sh��)���̺�����C��ֱ������(bi��o)���̣�
�ą���(sh��)���̺�����C��ֱ������(bi��o)���̣�
�����O(sh��)ֱ��![]() �c����C����P��Q���c(di��n)����
�c����C����P��Q���c(di��n)����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵxOy�У����E�A![]() ��ÿһ�c(di��n)�ęM����(bi��o)���ֲ�׃���v����(bi��o)׃?y��u)�ԭ����һ�룬������C��������(bi��o)ԭ�c(di��n)��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ��ֱ��l�ĘO����(bi��o)���̞�
��ÿһ�c(di��n)�ęM����(bi��o)���ֲ�׃���v����(bi��o)׃?y��u)�ԭ����һ�룬������C��������(bi��o)ԭ�c(di��n)��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ��ֱ��l�ĘO����(bi��o)���̞�![]() ��
��
![]() ��������C����ͨ���̺�ֱ��l��ֱ������(bi��o)���̣�
��������C����ͨ���̺�ֱ��l��ֱ������(bi��o)���̣�
![]() ��֪�c(di��n)
��֪�c(di��n)![]() ��ֱ��l�c����C����A��B���c(di��n)����
��ֱ��l�c����C����A��B���c(di��n)����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���p����C��![]() ���ҽ��c(di��n)�քe��
���ҽ��c(di��n)�քe��![]() ��
��![]() ��������c(di��n)�քe��
��������c(di��n)�քe��![]() ��B��̓�S������c(di��n)����ֱ��
��B��̓�S������c(di��n)����ֱ��![]() �ϴ��ڃ��c(di��n)
�ϴ��ڃ��c(di��n)![]() ʹ��
ʹ��![]() �����^�p�������ҽ��c(di��n)
�����^�p�������ҽ��c(di��n)![]() ��б�ʞ�1��ֱ���c�p���������҃�֧����һ�����c(di��n)���t�p�����x���ʵķ����ǣ� ��
��б�ʞ�1��ֱ���c�p���������҃�֧����һ�����c(di��n)���t�p�����x���ʵķ����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)ֱ��![]() �cƽ��
�cƽ��![]() �ཻ������ֱ���t�����f�������_���ǣ� ��
�ཻ������ֱ���t�����f�������_���ǣ� ��
A.��ƽ��![]() ��(n��i)�]��ֱ���cֱ��
��(n��i)�]��ֱ���cֱ��![]() ��ֱ��
��ֱ��
B.��ƽ��![]() ��(n��i)����ֻ��һ�lֱ���cֱ��
��(n��i)����ֻ��һ�lֱ���cֱ��![]() ��ֱ��
��ֱ��
C.��ƽ��![]() ��(n��i)�Пo��(sh��)�lֱ���cֱ��
��(n��i)�Пo��(sh��)�lֱ���cֱ��![]() ��ֱ��
��ֱ��
D.��ƽ��![]() ��(n��i)���ڃɗl�ֱཻ���cֱ��
��(n��i)���ڃɗl�ֱཻ���cֱ��![]() ��ֱ.
��ֱ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�AE�ķ��̞�![]() y2��1�������c(di��n)���ҽ��c(di��n)�քe��F1��F2��P�ǙE�AE��λ�ڵ�һ����һ�c(di��n)
y2��1�������c(di��n)���ҽ��c(di��n)�քe��F1��F2��P�ǙE�AE��λ�ڵ�һ����һ�c(di��n)
��1����������PF1F2����e��![]() �����c(di��n)P������(bi��o)��
�����c(di��n)P������(bi��o)��
��2���O(sh��)A��1��0����ӛ����PA���L�Ȟ�d����d����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���ڎ��w![]() �У���߅��
�У���߅��![]() �Ǿ��Σ�
�Ǿ��Σ�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �քe�Ǿ���
�քe�Ǿ���![]() ��
��![]() �����c(di��n).
�����c(di��n).

�������C��![]() ƽ��
ƽ��![]() ��
��
������ƽ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�����
�У�����![]() �ą���(sh��)������
�ą���(sh��)������ ��t�Dž���(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ������
��t�Dž���(sh��)����������(bi��o)ԭ�c(di��n)��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)������
�ĘO����(bi��o)������![]() ��
��
��1��������![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2������������c(di��n)��![]() ����
����![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�����֪�c(di��n)
�У�����֪�c(di��n)![]() ��
��![]() ��
��![]() ������
������![]() ����һ�c(di��n)��
����һ�c(di��n)��![]() ���c(di��n)
���c(di��n)![]() �ľ��x�͵��c(di��n)
�ľ��x�͵��c(di��n)![]() �ľ��x�ı�ֵ��2���ڈA
�ľ��x�ı�ֵ��2���ڈA![]() ��(j��ng)�^
��(j��ng)�^![]() ��
��![]() ���҈A����ֱ��
���҈A����ֱ��![]() ��.�Ģ٢������xһ���l��.
��.�Ģ٢������xһ���l��.
��1��������![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ������
������![]() �ص����L��2����
�ص����L��2����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com