
【題目】已知函數(shù)f(x)=|x﹣a|﹣|x﹣4a|(a>0),若對x∈R,都有f(2x)﹣1≤f(x),則實數(shù)a的最大值為( )
A.![]()
B.![]()
C.![]()
D.1
【答案】B
【解析】解:f(2x)﹣1≤f(x)恒成立,即|2x﹣a|﹣|2x﹣4a|﹣1≤|x﹣a|﹣|x﹣4a|恒成立,
即|2x﹣a|+|x﹣4a|≤|x﹣a|+|2x﹣4a|+1恒成立.
此不等式中,絕對值的“根”共有4個:![]() , a,2a,4a,
, a,2a,4a,
當x<![]() 時,不等式即 a﹣2x+4a﹣x≤a﹣x+4a﹣2x+1,即0≤1.
時,不等式即 a﹣2x+4a﹣x≤a﹣x+4a﹣2x+1,即0≤1.
當![]() ≤x<a時,不等式即 2x﹣a+4a﹣x≤a﹣x+4a﹣2x+1,即2x﹣
≤x<a時,不等式即 2x﹣a+4a﹣x≤a﹣x+4a﹣2x+1,即2x﹣![]() ≤a,故有2a﹣
≤a,故有2a﹣![]() ≤a,即a≤
≤a,即a≤![]() .
.
當a≤x<2a時,不等式即 2x﹣a+4a﹣x≤x﹣a+4a﹣2x+1,即x≤![]() .
.
當2a≤x<4a時,不等式即 2x﹣a+4a﹣x≤x﹣a+2x﹣4a+1,即 8a≤2x+1,故8a≤4a+1,可得a≤![]() .
.
當x≥4a時,不等式即 2x﹣a+x﹣4a≤a﹣x+2x﹣4a+1,即0≤1.
綜上可得,a≤![]() , 故a的最大值為
, 故a的最大值為![]() ,
,
故選:B.
【考點精析】本題主要考查了絕對值不等式的解法的相關(guān)知識點,需要掌握含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規(guī)律:關(guān)鍵是去掉絕對值的符號才能正確解答此題.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() ,
, ![]() 的圖象在點
的圖象在點 ![]() 處的切線為
處的切線為 ![]() .
.
(1)求函數(shù) ![]() 的解析式;
的解析式;
(2)若 ![]() 對任意的
對任意的 ![]() 恒成立,求實數(shù)
恒成立,求實數(shù) ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四棱錐![]() 中,側(cè)面
中,側(cè)面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證:PA//平面BEF;
(Ⅱ)若PC與AB所成角為![]() ,求
,求![]() 的長;
的長;
(Ⅲ)在(Ⅱ)的條件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】乒乓球比賽規(guī)則規(guī)定:一局比賽,雙方比分在10平前,一方連續(xù)發(fā)球2次后,對方再連續(xù)發(fā)球2次,依次輪換.每次發(fā)球,勝方得1分,負方得0分.設(shè)在甲、乙的比賽中,每次發(fā)球,發(fā)球方得1分的概率為0.6,各次發(fā)球的勝負結(jié)果相互獨立.甲、乙的一局比賽中,甲先發(fā)球.
(1)求開始第4次發(fā)球時,甲、乙的比分為1比2的概率;
(2)![]() 表示開始第4次發(fā)球時乙的得分,求
表示開始第4次發(fā)球時乙的得分,求 ![]() 的期望.
的期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】當|a|≤1,|x|≤1時,關(guān)于x的不等式|x2﹣ax﹣a2|≤m恒成立,則實數(shù)m的取值范圍是( )
A.[![]() , +∞)
, +∞)
B.[![]() , +∞)
, +∞)
C.[![]() , +∞)
, +∞)
D.[![]() , +∞)
, +∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(2015·新課標I卷)選修4-5:不等式選講
已知函數(shù)f(x)=|x+1|-2|x-a|, a>0.
(1)當a=1時求不等式f(x)>1的解集;
(2)若f(x)圖像與x軸圍成的三角形面積大于6,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 的一個內(nèi)角為
的一個內(nèi)角為![]() ,并且三邊長構(gòu)成公差為4的等差數(shù)列,則
,并且三邊長構(gòu)成公差為4的等差數(shù)列,則![]() 的面積為( )
的面積為( )
A. 15 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某農(nóng)科所對冬季晝夜溫差大小與某反季節(jié)大豆新品種發(fā)芽多少之間的關(guān)系進行分析研究,他們分別記錄了![]() 月
月![]() 日至
日至![]() 月
月![]() 日的每天晝夜溫差與實驗室每天每
日的每天晝夜溫差與實驗室每天每![]() 顆種子中的發(fā)芽數(shù),得到如下資料:
顆種子中的發(fā)芽數(shù),得到如下資料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
溫差 |
|
|
|
|
|
發(fā)芽數(shù) |
|
|
|
|
|
該農(nóng)科所確定的研究方案是:先從這![]() 組數(shù)據(jù)中選取
組數(shù)據(jù)中選取![]() 組,用剩下的
組,用剩下的![]() 組數(shù)據(jù)求線性回歸方程,再用被選取的
組數(shù)據(jù)求線性回歸方程,再用被選取的![]() 組數(shù)據(jù)進行檢驗.
組數(shù)據(jù)進行檢驗.
(1)求選取的![]() 組數(shù)據(jù)恰好是不相鄰
組數(shù)據(jù)恰好是不相鄰![]() 天的數(shù)據(jù)的概率;
天的數(shù)據(jù)的概率;
(2)若選取的是![]() 月
月![]() 日與
日與![]() 月
月![]() 日的兩組數(shù)據(jù),請根據(jù)
日的兩組數(shù)據(jù),請根據(jù)![]() 月
月![]() 日至
日至![]() 日的數(shù)據(jù),求出
日的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ,由線性回歸方程得到的估計數(shù)據(jù)與所選取的檢驗數(shù)據(jù)的誤差均不超過
,由線性回歸方程得到的估計數(shù)據(jù)與所選取的檢驗數(shù)據(jù)的誤差均不超過![]() 顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得試的線性回歸方程是否可靠?
顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得試的線性回歸方程是否可靠?
附: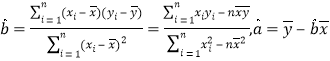
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com