
【題目】已知函數(shù)![]() ,
,![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)求證:當(dāng)![]() 時,
時,![]() ;
;
(2)若函數(shù)![]() 有兩個零點(diǎn),求實(shí)數(shù)
有兩個零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)構(gòu)造![]() ,再求導(dǎo)可得
,再求導(dǎo)可得![]() ,再對導(dǎo)數(shù)求導(dǎo),繼而分析導(dǎo)函數(shù)的正負(fù)區(qū)間進(jìn)而求得原函數(shù)的單調(diào)區(qū)間求最小值證明即可.
,再對導(dǎo)數(shù)求導(dǎo),繼而分析導(dǎo)函數(shù)的正負(fù)區(qū)間進(jìn)而求得原函數(shù)的單調(diào)區(qū)間求最小值證明即可.
(2) 求導(dǎo)可得![]() ,再分
,再分![]() ,
,![]() ,
,![]() 分析函數(shù)的最小值,同時根據(jù)零點(diǎn)存在性定理判斷是否有兩個零點(diǎn)即可.
分析函數(shù)的最小值,同時根據(jù)零點(diǎn)存在性定理判斷是否有兩個零點(diǎn)即可.
(1)設(shè)![]() …
…
∴![]() ,
,
∴![]()
∵![]() ∴
∴![]() ∴
∴![]()
∴![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
又![]()
∴![]() 時,
時,![]()
∴![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
又![]()
∴![]() 時,
時,![]()
故當(dāng)![]() 時,
時,![]() ;
;
(2)∵![]()
∴![]() ,
,
①當(dāng)![]() 時,易知函數(shù)
時,易知函數(shù)![]() 只有一個零點(diǎn),不符合題意;
只有一個零點(diǎn),不符合題意;
②當(dāng)![]() 時,在
時,在![]() 上,
上,![]() ,
,![]() 單調(diào)遞減;在
單調(diào)遞減;在![]() 上,
上,![]() ,
,![]() 單調(diào)遞增;又
單調(diào)遞增;又![]() ,且
,且![]() ,且當(dāng)
,且當(dāng)![]() 上,
上,![]() 恒成立,
恒成立,
又不妨取![]() 且
且![]() 時,
時,![]()
或者考慮:當(dāng)![]()
所以函數(shù)![]() 在
在![]() 和在
和在![]() 上各有一個零點(diǎn),即有兩個零點(diǎn).
上各有一個零點(diǎn),即有兩個零點(diǎn).
③當(dāng)![]() 時,由
時,由![]() 得
得![]() 或
或![]()
(i)當(dāng)![]() 即
即![]() 時,在
時,在![]() 上,
上,![]() 成立,故
成立,故![]() 在
在![]() 上單調(diào)遞增,所以函數(shù)
上單調(diào)遞增,所以函數(shù)![]() 至多有一個零點(diǎn),不符合題意
至多有一個零點(diǎn),不符合題意
(ii)當(dāng)![]() 即
即![]() 時,在
時,在![]() 和
和![]() 上,
上,![]() ,
,![]() 單調(diào)遞增;
單調(diào)遞增;
在![]() 上
上![]() ,
,![]() 單調(diào)遞減;
單調(diào)遞減;
又![]() ,且
,且![]() ,
,
所以函數(shù)![]() 至多有一個零點(diǎn),不符合題意
至多有一個零點(diǎn),不符合題意
(iii)當(dāng)![]() 即
即![]() 時,在
時,在![]() 和
和![]() 上
上![]() ,
,![]() 單調(diào)遞增;在
單調(diào)遞增;在![]() 上
上![]() ,
,![]() 單調(diào)遞減;又
單調(diào)遞減;又![]() ,所以函數(shù)
,所以函數(shù)![]() 至多有一個零點(diǎn),不符合題意
至多有一個零點(diǎn),不符合題意
綜上所述:實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 滿足:
滿足:![]() (常數(shù)
(常數(shù)![]() ),
),![]() ,(
,(![]() ,
,![]() ).數(shù)列
).數(shù)列![]() 滿足:
滿足:![]()
![]() .
.
(1)分別求![]() ,
,![]() ,
,![]() 的值:
的值:
(2)求數(shù)列![]() 的通項公式;
的通項公式;
(3)問:數(shù)列![]() 的每一項能否均為整數(shù)?若能,求出
的每一項能否均為整數(shù)?若能,求出![]() 的所有可能值;若不能,請說明理由.
的所有可能值;若不能,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】改革開放以來,我國農(nóng)村7億多貧困人口擺脫貧困,貧困發(fā)生率由1978年的97.5%下降到2018年底的1.4%,創(chuàng)造了人類減貧史上的中國奇跡,為全球減貧事業(yè)貢獻(xiàn)了中國智慧和中國方案.“貧困發(fā)生率”是指低于貧困線的人口占全體人口的比例.2012年至2018年我國貧困發(fā)生率的數(shù)據(jù)如下表:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
貧困發(fā)生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)從表中所給的7個貧困發(fā)生率數(shù)據(jù)中任選兩個,求至少有一個低于5%的概率;
(2)設(shè)年份代碼![]() ,利用回歸方程,分析2012年至2018年貧困發(fā)生率的變化情況,并預(yù)測2019年貧困發(fā)生率.
,利用回歸方程,分析2012年至2018年貧困發(fā)生率的變化情況,并預(yù)測2019年貧困發(fā)生率.
附:回歸直線![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: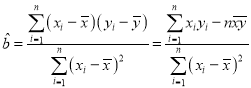 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形,![]() ,
,![]() 均為等邊三角形,
均為等邊三角形,![]() ,
,![]() .
.
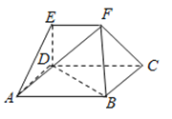
(Ⅰ)過![]() 作截面與線段
作截面與線段![]() 交于點(diǎn)
交于點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ,試確定點(diǎn)
,試確定點(diǎn)![]() 的位置,并予以證明;
的位置,并予以證明;
(Ⅱ)在(Ⅰ)的條件下,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=lnx+a(x2﹣1).
(1)討論函數(shù)f(x)的單調(diào)性;
(2)當(dāng)a![]() ,x∈[1,+∞)時,證明:f(x)≤(x﹣1)ex.
,x∈[1,+∞)時,證明:f(x)≤(x﹣1)ex.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右焦點(diǎn)F到左頂點(diǎn)的距離為3.
的右焦點(diǎn)F到左頂點(diǎn)的距離為3.
(1)求橢圓C的方程;
(2)設(shè)O是坐標(biāo)原點(diǎn),過點(diǎn)F的直線與橢圓C交于A,B兩點(diǎn)(A,B不在x軸上),若![]() ,延長AO交橢圓與點(diǎn)G,求四邊形AGBE的面積S的最大值.
,延長AO交橢圓與點(diǎn)G,求四邊形AGBE的面積S的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種產(chǎn)品的質(zhì)量以其質(zhì)量指標(biāo)值衡量,質(zhì)量指標(biāo)值越大表明質(zhì)量越好,記其質(zhì)量指標(biāo)值為M,當(dāng)M≥85時,產(chǎn)品為一級品;當(dāng)75≤M<85時,產(chǎn)品為二級品;當(dāng)70≤M<75時,產(chǎn)品為三級品.現(xiàn)用兩種新配方(分別稱為A配方和B配方)做實(shí)驗,各生產(chǎn)了100件這種產(chǎn)品,并測量了每件產(chǎn)品的質(zhì)量指標(biāo)值,得到下面試驗結(jié)果:
A配方的頻數(shù)分布表

B配方的頻數(shù)分布表

(1)從A配方生產(chǎn)的產(chǎn)品中按等級分層抽樣抽取5件產(chǎn)品,再從這5件產(chǎn)品中任取3件,求恰好取到1件二級品的頻率;
(2)若這種新產(chǎn)品的利潤率y與質(zhì)量指標(biāo)M滿足如下條件: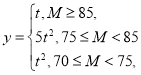 其中t∈
其中t∈![]() ,請分別計算兩種配方生產(chǎn)的產(chǎn)品的平均利潤率,如果從長期來看,你認(rèn)為投資哪種配方的產(chǎn)品平均利潤率較大?
,請分別計算兩種配方生產(chǎn)的產(chǎn)品的平均利潤率,如果從長期來看,你認(rèn)為投資哪種配方的產(chǎn)品平均利潤率較大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,滿足acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若△ABC的周長為3,求△ABC的內(nèi)切圓面積S的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是線段EF上的動點(diǎn)
AC,P是線段EF上的動點(diǎn)
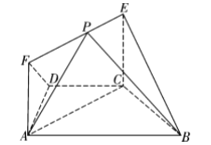
(1)求證:平面BCE⊥平面ACEF;
(2)求平面PAB與平面BCE所成銳二面角![]() 的最小值
的最小值
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com