【題目】已知一個口袋有
個白球，
個黑球，這些球除顏色外全部相同，現將口袋中的球隨機逐個取出，并依次放入編號為，
，，
的抽屜內.
（1）求編號為的抽屜內放黑球的概率；
（2）口袋中的球放入抽屜后，隨機取出兩個抽屜中的球，求取出的兩個球是一黑一白的概率.
【答案】(1) 
.(2) 
.
【解析】
(1)4個球放入編號為1，2，3，4的抽屜里，有4種方法，滿足題意的有1中，根據古典概型公式得到結果；（2）根據抽屜的編號，對于一種確定的放法，取法有6種情況，滿足一白一黑的有3種情況，進而得到結果.
（1）將口袋中的
個白球，
個黑球，依次放入編號為，
，，
的抽屜內，共有種不同的放法，分別是（白，白，白，黑），（白，白，黑，白），（白，黑，白，白），（黑，白，白，白），其中編號為的抽屜內放黑球的情況有種，所以編號為的抽屜內放黑球的概率為.
（2）假設口袋內的球逐個依次取出放入抽屜內后是（白，白，白，黑），隨機取出兩個球，根據抽屜的編號，可能是
，
，
，
，
，
共6種，其中一黑一白的是，，共種，所以取出的兩個球是一黑一白的概率為.
互動課堂系列答案
激活思維智能訓練課時導學練系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，在平行四邊形
中，
點
是
邊的中點，將
沿
折起，使點
到達點
的位置，且
（1）求證; 平面
平面
；
（2）若平面
和平面
的交線為
，求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】出租車幾何學是由十九世紀的赫爾曼·閔可夫斯基所創立的。在出租車幾何學中，點還是形如
的有序實數對，直線還是滿足
的所有組成的圖形，角度大小的定義也和原來一樣，直角坐標系內任意兩點
定義它們之間的一種“距離”：
，請解決以下問題：
（1）求線段
上一點
到點
的“距離”；
（2）定義：“圓”是所有到定點“距離”為定值的點組成的圖形，求“圓”上的所有點到點
的“距離”均為
的“圓”方程，并求該“圓”圍成的圖形的面積；
（3）若點
到點
的“距離”和點到點
的“距離”相等，其中實數
滿足
，求所有滿足條件的點
的軌跡的長之和.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著手機的普及，大學生迷戀手機的現象非常嚴重.為了調查雙休日大學生使用手機的時間，某機構采用不記名方式隨機調查了使用手機時間不超過
小時的
名大學生，將人使用手機的時間分成
組：
，
，
，
，
分別加以統計，得到下表，根據數據完成下列問題：
使用時間/時 |
|
|
|
|
|
大學生/人 |
|
|
|
|
|
（1）完成頻率分布直方圖；
（2）根據頻率分布直方圖估計大學生使用手機的平均時間.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示,已知點
是拋物線
上一定點,直線
的傾斜角互補,且與拋物線另交于
，
兩個不同的點．
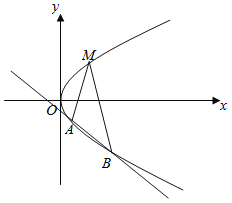
(1)求點
到其準線的距離；
(2)求證：直線
的斜率為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖甲所示，
是梯形
的高，
，
，
，先將梯形沿
折起如圖乙所示的四棱錐
，使得
.
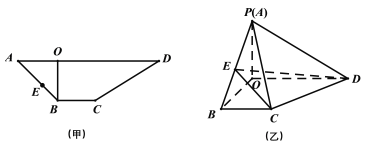
（1）在棱
上是否存在一點
，使得
平面
？若存在，請求出
的值，若不存在，請說明理由;
（2）點
是線段
上一動點，當直線
與
所成的角最小時，求二面角
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
