
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,點
上,點![]() 滿足以
滿足以![]() 為直徑的圓過橢圓的上頂點
為直徑的圓過橢圓的上頂點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() 過右焦點
過右焦點![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() 使得
使得![]() 為定值?如果存在,求出點
為定值?如果存在,求出點![]() 的坐標;如果不存在,說明理由.
的坐標;如果不存在,說明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)由點在橢圓上代入可得![]() ,
,![]() 的關系,再由點
的關系,再由點![]() 滿足以
滿足以![]() 為直徑的圓過橢圓的上頂點
為直徑的圓過橢圓的上頂點![]() .可得
.可得![]() 可得
可得![]() ,
,![]() 的關系,再由
的關系,再由![]() ,
,![]() ,
,![]() 的關系求出橢圓的方程;
的關系求出橢圓的方程;
(2)由(1)可得右焦點![]() 的坐標,分坐標
的坐標,分坐標![]() 的斜率為0和不為0兩種情況討論,假設存在
的斜率為0和不為0兩種情況討論,假設存在![]() 滿足條件,設直線
滿足條件,設直線![]() 的方程,與橢圓聯立求出兩根之和及兩根之積,進而求出數量積
的方程,與橢圓聯立求出兩根之和及兩根之積,進而求出數量積![]() 的表達式,要使數量積為定值,則分子分母對應項的系數成比例,可得
的表達式,要使數量積為定值,則分子分母對應項的系數成比例,可得![]() 的值,且可求出定值.
的值,且可求出定值.
解:(1)由題意可得上頂點![]() ,
,![]() ,所以:
,所以:![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() 即
即![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
所以橢圓的方程為:![]() ;
;
(2)由(1)可得右焦點![]() 的坐標
的坐標![]() ,假設存在
,假設存在![]()
![]() 當直線
當直線![]() 的斜率不為0時,設直線
的斜率不為0時,設直線![]() 的方程為:
的方程為:![]() ,設
,設![]() ,
,![]() ,
,![]() ,
,![]() ,
,
聯立直線與橢圓的方程![]() ,整理可得:
,整理可得:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
因為![]()
![]() ,
,
要使![]() 為定值,則
為定值,則![]() ,解得:
,解得:![]() ,這時
,這時![]() 為定值,
為定值,
![]() 當直線
當直線![]() 的斜率為0時,則
的斜率為0時,則![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
綜上所述:所以存在![]() ,
,![]() ,使
,使![]() 為定值.
為定值.


科目:高中數學 來源: 題型:
【題目】十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龍)、巳(蛇)、午(馬)、未(羊)、申(猴)、酉(雞)、戌(狗)、亥(豬),每一個人的出生年份對應了十二種動物中的一種,即自己的屬相.現有印著十二生肖圖案的毛絨娃娃各一個,小張同學的屬相為馬,小李同學的屬相為羊,現在這兩位同學從這十二個毛絨娃娃中各隨機取一個(不放回),則這兩位同學都拿到自己屬相的毛絨娃娃的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著5G商用進程的不斷加快,手機廠商之間圍繞5G用戶的爭奪越來越激烈,5G手機也頻頻降低身價飛人尋常百姓家.某科技公司為了給自己新推出的5G手機定價,隨機抽取了100人進行調查,對其在下一次更換5G手機時,能接受的價格(單位:元)進行了統計,得到結果如下表,已知這100個人能接受的價格都在![]() 之間,并且能接受的價格的平均值為2350元(同一組的數據用該組區間的中點值代替).
之間,并且能接受的價格的平均值為2350元(同一組的數據用該組區間的中點值代替).
分組 | 一 | 二 | 三 | 四 | 五 |
手機價格X(元) |
|
|
|
|
|
頻數 | 10 | x | y | 20 | 20 |
(1)現用分層抽樣的方法從第一、二、三組中隨機抽取6人,將該樣本看成一個總體,從中隨機抽取2人,求其中恰有1人能接受的價格不低于2000元的概率;
(2)若人們對5G手機能接受的價格X近似服從正態分布![]() ,其中
,其中![]() 為樣本平均數
為樣本平均數![]() ,
,![]() 為樣本方差
為樣本方差![]() ,求
,求![]() .
.
附:![]() .若
.若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年2月13日《西安市全民閱讀促進條例》全文發布,旨在保障全民閱讀權利,培養全民閱讀習慣,提高全民閱讀能力,推動文明城市和文化強市建設.某高校為了解條例發布以來全校學生的閱讀情況,隨機調查了200名學生每周閱讀時間![]() (單位:小時)并繪制如圖所示的頻率分布直方圖.
(單位:小時)并繪制如圖所示的頻率分布直方圖.
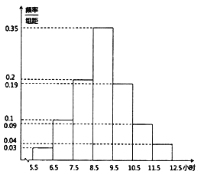
(1)求這200名學生每周閱讀時間的樣本平均數;
(2)為查找影響學生閱讀時間的因素,學校團委決定從每周閱讀時間為![]() ,
,![]() 的學生中抽取9名參加座談會.
的學生中抽取9名參加座談會.
(i)你認為9個名額應該怎么分配?并說明理由;
(ii)座談中發現9名學生中理工類專業的較多.請根據200名學生的調研數據,填寫下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為學生閱讀時間不足(每周閱讀時間不足8.5小時)與“是否理工類專業”有關?(精確到0.1)
的把握認為學生閱讀時間不足(每周閱讀時間不足8.5小時)與“是否理工類專業”有關?(精確到0.1)
閱讀時間不足8.5小時 | 閱讀時間超過8.5小時 | |
理工類專業 | 40 | 60 |
非理工類專業 |
附: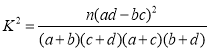 (
(![]() ).
).
臨界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 的焦點為
的焦點為![]() ,準線為
,準線為![]() ,過點
,過點![]() 的直線交拋物線于
的直線交拋物線于![]() ,
,![]() 兩點,點
兩點,點![]() 在準線
在準線![]() 上的投影為
上的投影為![]() ,點
,點![]() 是拋物線上一點,且滿足
是拋物線上一點,且滿足![]() .
.
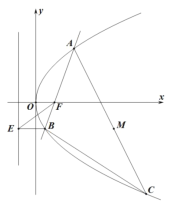
(1)若點![]() 坐標是
坐標是![]() ,求線段
,求線段![]() 中點
中點![]() 的坐標;
的坐標;
(2)求![]() 面積的最小值及此時直線
面積的最小值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓臺側面的母線長為![]() ,母線與軸的夾角為
,母線與軸的夾角為![]() ,一個底面的半徑是另一個底面半徑的
,一個底面的半徑是另一個底面半徑的![]() 倍.
倍.

(1)求圓臺兩底面的半徑;
(2)如圖,點![]() 為下底面圓周上的點,且
為下底面圓周上的點,且![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,CM,CN為某公園景觀湖胖的兩條木棧道,∠MCN=120°,現擬在兩條木棧道的A,B處設置觀景臺,記BC=a,AC=b,AB=c(單位:百米)
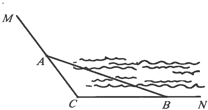
(1)若a,b,c成等差數列,且公差為4,求b的值;
(2)已知AB=12,記∠ABC=θ,試用θ表示觀景路線A-C-B的長,并求觀景路線A-C-B長的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com