
【題目】已知關于![]() 的函數
的函數![]() 為
為![]() 上的偶函數,且在區間
上的偶函數,且在區間![]() 上的最大值為10. 設
上的最大值為10. 設![]() .
.
⑴ 求函數![]() 的解析式;
的解析式;
⑵ 若不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
⑶ 是否存在實數![]() ,使得關于
,使得關于![]() 的方程
的方程![]() 有四個不相等的實 數根?如果存在,求出實數
有四個不相等的實 數根?如果存在,求出實數![]() 的范圍,如果不存在,說明理由.
的范圍,如果不存在,說明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案見解析.
;(3)答案見解析.
【解析】【試題分析】(1)利用![]() ,化簡后可求得
,化簡后可求得![]() .此時函數對稱軸為
.此時函數對稱軸為![]() 軸,故當
軸,故當![]() 時取得最大值,由此求得
時取得最大值,由此求得![]() .進而求得
.進而求得![]() .(2)將原不等式分離參數得到
.(2)將原不等式分離參數得到![]() 在
在![]() 上恒成立,利用換元法結合二次函數最值可求得
上恒成立,利用換元法結合二次函數最值可求得![]() .(3)先將原方程化為
.(3)先將原方程化為![]() .利用換元法令
.利用換元法令![]() ,將上式變為二次函數零點問題來求解.
,將上式變為二次函數零點問題來求解.
【試題解析】
(1)∵![]() 為
為![]() 上的偶函數,
上的偶函數, ![]() ,
,
![]() ,
, ![]() 關于
關于![]() 恒成立,
恒成立, ![]()
![]() ,
, ![]() 在區間
在區間![]() 上的最大值為10,
上的最大值為10,
![]() 當
當![]() 時,
時, ![]() 解得:
解得: ![]() ,
,
![]()
![]()
(2)不等式![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
上式可化為![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,∵
,∵![]() ,∴
,∴![]() ,則
,則![]() 在
在![]() 上恒成立,
上恒成立,
又∵當![]() 時,
時, ![]() ,∴
,∴![]() ,即所求實數
,即所求實數![]() 的取值范圍為
的取值范圍為![]()
(3)方程![]() ,即
,即![]() ,
,
可化為: ![]() ,
,
令![]() ,則
,則![]() ,
,
若關于![]() 的方程
的方程![]() 有四個不相等的實數根,
有四個不相等的實數根,
則關于![]() 的方程
的方程![]() 必須有兩個不相等的實數根
必須有兩個不相等的實數根![]() 和
和![]() ,
,
并且![]() ,記
,記![]()
![]() ,
,
則, 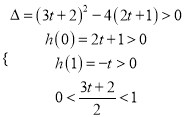
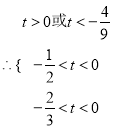 解得:
解得: ![]() ,所以,存在實數
,所以,存在實數![]() 使得關于
使得關于![]() 的方程
的方程
![]() 有四個不相等的實數根,
有四個不相等的實數根, ![]() 取值范圍為
取值范圍為![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx+ ![]() ,(a>0)
,(a>0)
(1)當a=2時,求函數f(x)在x=1處的切線方程;
(2)若函數f(x)在區間[1,+∞)上單調遞增,求a的取值范圍;
(3)求函數f(x)在區間[1,2]的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產A,B兩種產品,根據市場調查與預測,A產品的利潤與投資成正比,其關系如圖①;B產品的利潤與投資的算術平方根成正比,其關系如圖②.(注:利潤和投資單位:萬元)
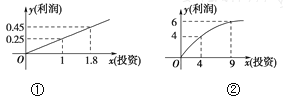
(1)分別將A,B兩種產品的利潤表示為投資的函數關系式;
(2)已知該企業已籌集到18萬元資金,并將全部投入A,B兩種產品的生產,怎樣分配這18萬元投資,才能使該企業獲得最大利潤?其最大利潤約為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別為△ABC三個內角A,B,C的對邊,ccosA+ ![]() csinA﹣b﹣a=0.
csinA﹣b﹣a=0.
(Ⅰ)求C;
(Ⅱ)若c=1,求△ABC的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠擬建一個下部為圓柱,上部為半球的容器(如圖,圓柱高為h,半徑為r,不計厚度,單位:米),按計劃容積為72π立方米,且h≥2r,假設其建造費用僅與表面積有關(圓柱底部不計),已知圓柱部分每平方米的費用為2千元,半球部分每平方米4千元,設該容器的建造費用為y千元.
(Ⅰ)求y關于r的函數關系,并求其定義域;
(Ⅱ)求建造費用最小時的r.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心為
的圓心為![]() ,且截
,且截![]() 軸所得的弦長為
軸所得的弦長為![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)設圓![]() 與
與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,過
,過![]() 分別作斜率為
分別作斜率為![]() 的兩條直線交圓
的兩條直線交圓![]() 于
于![]() 兩點,且
兩點,且![]() ,試證明直線
,試證明直線![]() 恒過一定點,并求出該定點坐標.
恒過一定點,并求出該定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:x﹣2y+2m﹣2=0.
(1)求過點(2,3)且與直線l垂直的直線的方程;
(2)若直線l與兩坐標軸所圍成的三角形的面積大于4,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com