
【題目】已知圓![]() 的圓心為
的圓心為![]() ,且截
,且截![]() 軸所得的弦長為
軸所得的弦長為![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)設(shè)圓![]() 與
與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,過
,過![]() 分別作斜率為
分別作斜率為![]() 的兩條直線交圓
的兩條直線交圓![]() 于
于![]() 兩點,且
兩點,且![]() ,試證明直線
,試證明直線![]() 恒過一定點,并求出該定點坐標(biāo).
恒過一定點,并求出該定點坐標(biāo).
【答案】(1)![]() ;(2)
;(2)![]()
【解析】【試題分析】(1)設(shè)圓![]() 的半徑為
的半徑為![]() ,利用弦長和勾股定理,列方程可求得半徑為
,利用弦長和勾股定理,列方程可求得半徑為![]() ,進(jìn)而求得圓的方程.(2)在圓方程中,令
,進(jìn)而求得圓的方程.(2)在圓方程中,令![]() 求得
求得![]() 點坐標(biāo).寫出直線
點坐標(biāo).寫出直線![]() 的方程,聯(lián)立直線方程和圓的方程求得
的方程,聯(lián)立直線方程和圓的方程求得![]() 點的坐標(biāo),同理求得
點的坐標(biāo),同理求得![]() 點的坐標(biāo),求出直線
點的坐標(biāo),求出直線![]() 的斜率,從而得到直線
的斜率,從而得到直線![]() 的方程,化簡整理后可得定點為
的方程,化簡整理后可得定點為![]() .
.
【試題解析】
(1)設(shè)圓![]() 的半徑為
的半徑為![]() ,則
,則![]() ,所以
,所以![]() ,
,
所以圓![]() 的方程為
的方程為![]() .
.
(2)在![]() 中,令
中,令![]() 得
得![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]()
設(shè)![]() ,
, ![]() ,直線
,直線![]() 的方程為
的方程為![]() ,
,
由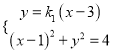 ,得
,得![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]()
所以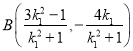 ,因為
,因為![]() ,所以
,所以![]() ,
,
用![]() 代替
代替![]() ,得
,得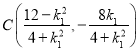 ,所以
,所以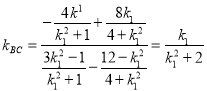
故直線![]() 的方程為
的方程為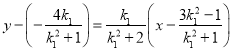 .
.
整理得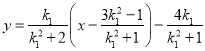
即![]() ,所以直線
,所以直線![]() 恒過一定點,定點為
恒過一定點,定點為![]() .
.


 全程金卷系列答案
全程金卷系列答案 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓 ![]() 的兩頂點為A,B如圖,離心率為
的兩頂點為A,B如圖,離心率為 ![]() ,過其焦點F(0,1)的直線l與橢圓交于C,D兩點,并與x軸交于點P,直線AC與直線BD交于點Q.
,過其焦點F(0,1)的直線l與橢圓交于C,D兩點,并與x軸交于點P,直線AC與直線BD交于點Q.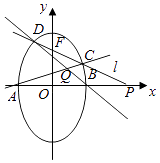
(Ⅰ)當(dāng) ![]() 時,求直線l的方程;
時,求直線l的方程;
(Ⅱ)當(dāng)點P異于A,B兩點時,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知關(guān)于![]() 的函數(shù)
的函數(shù)![]() 為
為![]() 上的偶函數(shù),且在區(qū)間
上的偶函數(shù),且在區(qū)間![]() 上的最大值為10. 設(shè)
上的最大值為10. 設(shè)![]() .
.
⑴ 求函數(shù)![]() 的解析式;
的解析式;
⑵ 若不等式![]() 在
在![]() 上恒成立,求實數(shù)
上恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
⑶ 是否存在實數(shù)![]() ,使得關(guān)于
,使得關(guān)于![]() 的方程
的方程![]() 有四個不相等的實 數(shù)根?如果存在,求出實數(shù)
有四個不相等的實 數(shù)根?如果存在,求出實數(shù)![]() 的范圍,如果不存在,說明理由.
的范圍,如果不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
![]() 是定義在
是定義在![]() 上的奇函數(shù).
上的奇函數(shù).
(1)求![]() 的值和實數(shù)
的值和實數(shù)![]() 的值;
的值;
(2)判斷函數(shù)![]() 在
在![]() 上的單調(diào)性,并給出證明;
上的單調(diào)性,并給出證明;
(3)若![]() 且
且![]() 求實數(shù)
求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
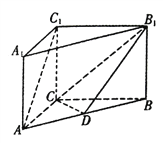
【題目】直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,點
,點![]() 是線段
是線段![]() 上的動點.
上的動點.
(1)當(dāng)點![]() 是
是![]() 的中點時,求證:
的中點時,求證: ![]() 平面
平面![]() ;
;
(2)線段![]() 上是否存在點
上是否存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,試求出
?若存在,試求出![]() 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐 ![]() 中,底面
中,底面 ![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)證明:平面 ![]() 平面
平面 ![]() ;
;
(Ⅱ)若二面角 ![]() 為
為 ![]() ,求
,求 ![]() 與平面
與平面 ![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知某射擊運(yùn)動員每次擊中目標(biāo)的概率都是0.7.現(xiàn)采用隨機(jī)模擬的方法估計該運(yùn)動員射擊4次,至少擊中2次的概率:先由計算器算出0~9之間取整數(shù)值的隨機(jī)數(shù),指定0,1,2表示沒有擊中目標(biāo),3,4,5,6,7,8,9表示擊中目標(biāo);因為射擊4次,故以每4個隨機(jī)數(shù)為一組,代表射擊4次的結(jié)果.經(jīng)隨機(jī)模擬產(chǎn)生了20組隨機(jī)數(shù):
5727 0293 7140 9857 0347
4373 8636 9647 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 6710 4281
據(jù)此估計,該射擊運(yùn)動員射擊4次至少擊中2次的概率為( )
A. 0.8 B. 0.85 C. 0.9 D. 0.95
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 年初的時候,國家政府工作報告明確提出,
年初的時候,國家政府工作報告明確提出, ![]() 年要堅決打好藍(lán)天保衛(wèi)戰(zhàn),加快解決燃煤污染問題,全面實施散煤綜合治理.實施煤改電工程后,某縣城的近六個月的月用煤量逐漸減少,
年要堅決打好藍(lán)天保衛(wèi)戰(zhàn),加快解決燃煤污染問題,全面實施散煤綜合治理.實施煤改電工程后,某縣城的近六個月的月用煤量逐漸減少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一個數(shù)據(jù)丟失,但根據(jù)
中一個數(shù)據(jù)丟失,但根據(jù)![]() 至
至![]() 月份的數(shù)據(jù)得出
月份的數(shù)據(jù)得出![]() 樣本平均值是
樣本平均值是![]() ,求出丟失的數(shù)據(jù);
,求出丟失的數(shù)據(jù);
(2)請根據(jù)![]() 至
至![]() 月份的數(shù)據(jù),求出
月份的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)現(xiàn)在用(2)中得到的線性回歸方程中得到的估計數(shù)據(jù)與![]() 月
月![]() 月的實際數(shù)據(jù)的誤差來判斷該地區(qū)的改造項目是否達(dá)到預(yù)期,若誤差均不超過
月的實際數(shù)據(jù)的誤差來判斷該地區(qū)的改造項目是否達(dá)到預(yù)期,若誤差均不超過![]() ,則認(rèn)為該地區(qū)的改造已經(jīng)達(dá)到預(yù)期,否則認(rèn)為改造未達(dá)預(yù)期,請判斷該地區(qū)的煤改電項目是否達(dá)預(yù)期?
,則認(rèn)為該地區(qū)的改造已經(jīng)達(dá)到預(yù)期,否則認(rèn)為改造未達(dá)預(yù)期,請判斷該地區(qū)的煤改電項目是否達(dá)預(yù)期?
(參考公式:線性回歸方程![]() ,其中
,其中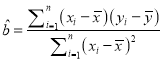
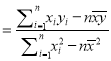 )
)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com