考點:利用導數求閉區間上函數的最值,利用導數研究函數的極值
專題:導數的綜合應用
分析:(1)求出函數的導數,利用導數大于0與小于0,判斷好的單調性,求出從而求極值及單調區間;
(2)求g′(x),通過討論a的值,導數分子的函數值的符號,判斷函數的極值點求解即可.
解答:
解:(1)f′(x)=-
.f′(x)>0,-3<x<-1,f′(x)<0,x<-3,-1<x<0,x>0.
| x | -4 | (-4,-3) | -3 | (-3,-1) | -1 | (-1,-) | - |
| f′(x) | | - | 0 | + | 0 | - | |
| f(x) | - |
Φ | 極小值
- | ↑ | 極大值0 | ↓ | -2 |
∴最大值為0,最小值為-2.
(2)g′(x)=-
.設u=x
2+4x+3a.△=16-12a,
當a≥
時,△≤0,g′(x)≤0,所以y=g(x)沒有極值點.
當0<a<
時,x
1=-2-
,x
2=-2+
<0.
減區間:(-∞,x
1),(x
2,0),(0,+∞),增區間:(x
1,x
2).∴有兩個極值點x
1,x
2.
當a=0時,g(x)=
+
,g′(x)=-
.
減區間:(-∞,-4),(0,+∞),增區間:(-4,0).∴有一個極值點x=-4.
綜上所述:a=0時,∴有一個極值點x=-4;0<a<
時有兩個極值點x=-2±
;a≥
時沒有極值點.
點評:本題主要考查了利用導數求函數的極值,函數的單調性,一般有解求參數問題常常將參數進行分離,轉化成研究已知函數在某個區間上的最值問題,屬于中檔題.



 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案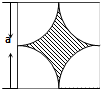 如圖所示,墻上掛有邊長為a的正方形木板,它的四個角的空白部分都是以正方形的頂點為圓心,半徑為
如圖所示,墻上掛有邊長為a的正方形木板,它的四個角的空白部分都是以正方形的頂點為圓心,半徑為