
【題目】在如圖所示的幾何體中,四邊形![]() 為平行四邊形,
為平行四邊形, ![]() 平面
平面![]() ,且
,且![]() 是
是![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值的大小.
的余弦值的大小.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)取AD的中點N,連接MN、NF.由三角形中位線定理,結合已知條件,證出四邊形MNFE為平行四邊形,從而得到EM∥FN,結合線面平行的判定定理,證出EM∥平面ADF;(2)求出平面ADF、平面BDF的一個法向量,利用向量的夾角公式,可求二面角![]() 的大小.
的大小.
解析:
(1)解法一:取![]() 的中點
的中點![]() ,連接
,連接![]() .
.
在![]() 中,
中, ![]() 是
是![]() 的中點,
的中點, ![]() 是
是![]() 的中點,
的中點,
所以![]() ,又因為
,又因為![]() ,
,
所以![]() 且
且![]() .
.
所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,
,
又因為![]() 平面
平面![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
解法二:因為![]() 平面
平面![]() ,
,
故以![]() 為原點,建立如圖所示的空間直角坐標系
為原點,建立如圖所示的空間直角坐標系![]() .
.
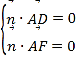
由已知可得![]() ,
,
設平面![]() 的一個法向量是
的一個法向量是![]() .
.
由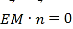 得
得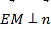
令![]() ,則
,則![]() .
.
又因為![]() ,所以
,所以![]() ,又
,又![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.
(2)由(1)可知平面![]() 的一個法向量是
的一個法向量是![]() .
.
易得平面![]() 的一個法向量是
的一個法向量是![]()
所以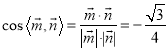 ,又二面角
,又二面角![]() 為銳角,
為銳角,
故二面角![]() 的余弦值大小為
的余弦值大小為![]() .
.


科目:高中數學 來源: 題型:
【題目】某集團為了獲得更大的收益,每年要投入一定的資金用于廣告促銷.經調查投入廣告費t(百萬元),可增加銷售額約為-t2+5t(百萬元)(0≤t≤5) (注:收益=銷售額-投放).
(1)若該公司將當年的廣告費控制在3百萬元之內,則應投入多少廣告費,才能使該公司由此獲得的收益最大?
(2)現該公司準備共投入3百萬元,分別用于廣告促銷和技術改造.經預測,每投入技術改造費x(百萬元),可增加的銷售額約為-![]() x3+x2+3x(百萬元).請設計一個資金分配方案,使該公司由此獲得的收益最大.
x3+x2+3x(百萬元).請設計一個資金分配方案,使該公司由此獲得的收益最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高鐵是我國國家名片之一,高鐵的修建凝聚著中國人的智慧與汗水.如圖所示,B、E、F為山腳兩側共線的三點,在山頂A處測得這三點的俯角分別為![]() 、
、![]() 、
、![]() ,計劃沿直線BF開通穿山隧道,現已測得BC、DE、EF三段線段的長度分別為3、1、2.
,計劃沿直線BF開通穿山隧道,現已測得BC、DE、EF三段線段的長度分別為3、1、2.

(1)求出線段AE的長度;
(2)求出隧道CD的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現安排甲、乙、丙、丁、戊5名同學參加2022年杭州亞運會志愿者服務活動,有翻譯、導游、禮儀、司機四項工作可以安排,以下說法正確的是( )
A. 每人都安排一項工作的不同方法數為![]()
B. 每項工作至少有一人參加,則不同的方法數為![]()
C. 如果司機工作不安排,其余三項工作至少安排一人,則這5名同學全部被安排的不同方法數為![]()
D. 每項工作至少有一人參加,甲、乙不會開車但能從事其他三項工作,丙、丁、戊都能勝任四項工作,則不同安排方案的種數是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的個數是( )
(1) 已知![]() ,
,![]() ,
,![]() ,則
,則![]()
(2)將6個相同的小球放入4個不同的盒子中,要求不出現空盒,共有10種放法.
(3) ![]() 被
被![]() 除后的余數為
除后的余數為![]() .
.
(4) 若![]() ,則
,則![]() =
=![]()
(5)拋擲兩個骰子,取其中一個的點數為點![]() 的橫坐標,另一個的點數為點
的橫坐標,另一個的點數為點![]() 的縱坐標,連續拋擲這兩個骰子三次,點
的縱坐標,連續拋擲這兩個骰子三次,點![]() 在圓
在圓![]() 內的次數
內的次數![]() 的均值為
的均值為![]()
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在![]() 上的函數
上的函數![]() 和數列
和數列![]() 滿足下列條件:
滿足下列條件:![]() ,
,![]() ,當
,當![]() 且
且![]() 時,
時,![]() 且
且![]() ,其中
,其中![]() 、
、![]() 均為非零常數.
均為非零常數.
(1)若![]() 是等差數列,求實數
是等差數列,求實數![]() 的值;
的值;
(2)令![]() (
(![]() ),若
),若![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(3)令![]() (
(![]() ),若
),若![]() ,數列
,數列![]() 滿足
滿足![]() ,若數列
,若數列![]() 有最大值
有最大值![]() ,最小值
,最小值![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 若命題![]() 都是真命題,則命題“
都是真命題,則命題“![]() ”為真命題
”為真命題
B. 命題“![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. 命題:“若![]() ,則
,則![]() 或
或![]() ”的否命題為“若
”的否命題為“若![]() ,則
,則![]() 或
或![]() ”
”
D. “![]() ”是“
”是“![]() ”的必要不充分條件
”的必要不充分條件
查看答案和解析>>
科目:高中數學 來源: 題型:
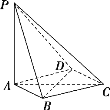
【題目】如圖,在四棱錐PABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
(1)求證:BD⊥平面PAC;
(2)若PA=4,求平面PBC與平面PDC所成角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com