
【題目】某高校健康社團為調查本校大學生每周運動的時長,隨機選取了80名學生,調查他們每周運動的總時長(單位:小時),按照![]()
![]()
![]()
![]()
![]()
![]() 共6組進行統計,得到男生、女生每周運動的時長的統計如下(表1、2),規定每周運動15小時以上(含15小時)的稱為“運動合格者”,其中每周運動25小時以上(含25小時)的稱為“運動達人”.
共6組進行統計,得到男生、女生每周運動的時長的統計如下(表1、2),規定每周運動15小時以上(含15小時)的稱為“運動合格者”,其中每周運動25小時以上(含25小時)的稱為“運動達人”.
表1:男生
時長 |
|
|
|
|
|
|
人數 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
時長 |
|
|
|
|
|
|
人數 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)從每周運動時長不小于20小時的男生中隨機選取2人,求選到“運動達人”的概率;
(2)根據題目條件,完成下面![]() 列聯表,并判斷能否有99%的把握認為本校大學生是否為“運動合格者”與性別有關.
列聯表,并判斷能否有99%的把握認為本校大學生是否為“運動合格者”與性別有關.
每周運動的時長小于15小時 | 每周運動的時長不小于15小時 | 總計 | |
男生 | |||
女生 | |||
總計 | |||
參考公式: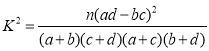 ,其中
,其中![]() .
.
參考數據:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |
【答案】(1)![]() ;(2)填表見解析,沒有99%的把握認為本校大學生是否為“運動合格者”與性別有關.
;(2)填表見解析,沒有99%的把握認為本校大學生是否為“運動合格者”與性別有關.
【解析】
(1)由題可知共有![]() 個基本事件,“運動達人”的可能結果為
個基本事件,“運動達人”的可能結果為![]() 個,
個,
求得概率即可;
(2)根據題意列出![]() 列聯表,代入公式計算結果,然后判斷即可.
列聯表,代入公式計算結果,然后判斷即可.
(1)每周運動的時長在![]() 中的男生有4人,在
中的男生有4人,在![]() 中的男生有2人,
中的男生有2人,
則共有![]() 個基本事件,
個基本事件,
其中![]() 中至少有1人被抽到的可能結果有
中至少有1人被抽到的可能結果有
![]() 個,
個,
所以抽到“運動達人”的概率為![]() ;
;
(2)每周運動的時長小于15小時的男生有26人,女生有16人;
每周運動的時長不小于15小時的男生有14人,女生有24人.
可得下列![]() 列聯表:
列聯表:
每周運動的時長小于15小時 | 每周運動的時長不小于15小時 | 總計 | |
男生 | 26 | 14 | 40 |
女生 | 16 | 24 | 40 |
總計 | 42 | 38 | 80 |
![]()
![]()
所以沒有99%的把握認為本校大學生是否為“運動合格者”與性別有關.


科目:高中數學 來源: 題型:
【題目】若一個四位數的各位數字相加和為10,則稱該數為“完美四位數”,如數字“2017”.試問用數字0,1,2,3,4,5,6,7組成的無重復數字且大于2017的“完美四位數”有( )個.
A. 71B. 66C. 59D. 53
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《孫子算經》是中國古代重要的數學著作,書中有一問題:“今有方物一束,外周一匝有三十二枚,問積幾何?”,該著作中提出了一種解決此問題的方法:“重置二位,左位減八,余加右位,至盡虛減一,即得.”通過對該題的研究發現,若一束方物外周一匝的枚數![]() 是8的整數倍時,均可采用此方法求解,如圖是解決這類問題的程序框圖,若輸入
是8的整數倍時,均可采用此方法求解,如圖是解決這類問題的程序框圖,若輸入![]() ,則輸出的結果為( )
,則輸出的結果為( )
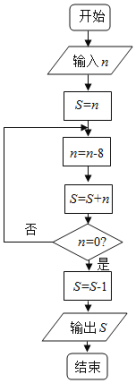
A.80B.47C.79D.48
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】算籌是在珠算發明以前我國獨創并且有效的計算工具,為我國古代數學的發展做出了很大貢獻.在算籌計數法中,以“縱式”和“橫式”兩種方式來表示數字,如圖:

表示多位數時,個位用縱式,十位用橫式,百位用縱式,千位用橫式,以此類推,遇零則置空,如圖:
![]()
如果把5根算籌以適當的方式全部放入 下面的表格中,那么可以表示的三位數的個數為( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱柱ABCD-![]() 中,地面ABCD為直角梯形,AB∥CD,AB⊥BC,平面ABCD⊥平面AB
中,地面ABCD為直角梯形,AB∥CD,AB⊥BC,平面ABCD⊥平面AB![]() ,∠BA
,∠BA![]() =60°,AB=A
=60°,AB=A![]() =2BC=2CD=2
=2BC=2CD=2
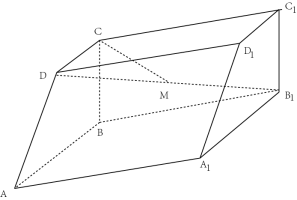
(1)求證:BC⊥A![]() ;
;
(2)求二面角D-A![]() -B的余弦值;
-B的余弦值;
(3)在線段D![]() 上是否存在點M,使得CM∥平面DA
上是否存在點M,使得CM∥平面DA![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生物興趣小組對冬季晝夜溫差與反季節新品種大豆發芽數之間的關系進行研究,他們分別記錄了![]() 月
月![]() 日至
日至![]() 月
月![]() 日每天的晝夜溫差與實驗室每天
日每天的晝夜溫差與實驗室每天![]() 顆種子的發芽數,得到以下表格
顆種子的發芽數,得到以下表格

該興趣小組確定的研究方案是:先從這![]() 組數據中選取
組數據中選取![]() 組數據,然后用剩下的
組數據,然后用剩下的![]() 組數據求線性回歸方程,再用被選取的
組數據求線性回歸方程,再用被選取的![]() 組數據進行檢驗.
組數據進行檢驗.
(1) 求統計數據中發芽數的平均數與方差;
(2) 若選取的是![]() 月
月![]() 日與
日與![]() 月
月![]() 日的兩組數據,請根據
日的兩組數據,請根據![]() 月
月![]() 日至
日至![]() 月
月![]() 日的數據,求出發芽數
日的數據,求出發芽數![]() 關于溫差
關于溫差![]() 的線性回歸方程
的線性回歸方程![]() ,若由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差不超過
,若由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差不超過![]() ,則認為得到的線性回歸方程是可靠的,問得到的線性回歸方程是否可靠? 附:線性回歸方程
,則認為得到的線性回歸方程是可靠的,問得到的線性回歸方程是否可靠? 附:線性回歸方程![]() 中斜率和截距最小二乘估法計算公式:
中斜率和截距最小二乘估法計算公式:
 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中真命題的個數是![]()
![]()
![]() 中,
中,![]() 是
是![]() 的三內角A,B,C成等差數列的充要條件;
的三內角A,B,C成等差數列的充要條件;
![]() 若“
若“![]() ,則
,則![]() ”的逆命題為真命題;
”的逆命題為真命題;
![]() 是
是![]() 或
或![]() 充分不必要條件;
充分不必要條件;
![]() 是
是![]() 的充要條件.
的充要條件.
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年5月,重慶市育才中學開展了“最美教室”文化布置評比活動,工作人員隨機抽取了16間教室進行量化評估,其中評分不低于9分的教室評為優秀,以下表格記錄了它們的評分情況:
分數段 |
|
|
|
|
教室間數 | 1 | 3 | 8 | 4 |
(1)現從16間教室隨機抽取3個,求至多有1個優秀的概率;
(2)以這16間教室評分數據估計全校教室的布置情況,若從全校所有教室中任選3個,記![]() 表示抽到優秀的教室個數,求
表示抽到優秀的教室個數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com