
【題目】已知函數 ![]() .
.
(1)當a>0時,求函數f(x)的單調區間;
(2)若f(x)在[1,e]上的最小值為1,求實數a的取值范圍;(其中e為自然對數的底數);
(3)若 ![]() 上恒成立,求實數a的取值范圍.
上恒成立,求實數a的取值范圍.
【答案】
(1)解:∵f'(x)= ![]() (x>0)
(x>0)
∴f'(x)>0x>a,f'(x)<00<x<a
∴f(x)在(0,a)上單調遞減,
在(a,+∞)上單調遞增
(2)解:∵x∈[1,e]
∴當a≤1時,f'(x)≥0,
∴f(x)在[1,e]上單調遞增,
故f(x)min=f(1)=a=1
滿足題意
當a≥e時,f'(x)≤0,
∴ ![]() a=0(舍去)
a=0(舍去)
當1<a<e時,由(1)知f(x)在(1,a)上單調遞減,
在(a,e)上單調遞增,
故f(x)min=f(a)=lna+1=1a=1(舍去)
綜上所述,a=1
(3)解:f(x)< ![]() x在(1,+∞)上恒成立a<
x在(1,+∞)上恒成立a< ![]() ﹣xlnx在(1,+∞)上恒成立
﹣xlnx在(1,+∞)上恒成立
![]()
g'(x)=x﹣lnx﹣1
令h(x)=x﹣lnx﹣1h'(x)
=1﹣ ![]()
當x∈(1,+∞)時,h'(x)>0
故h(x)在(1,+∞)上單調遞增,
所以h(x)>h(1)=0
![]() ,
,
所以a≤ ![]()
【解析】(1)由f'(x)= ![]() (x>0),能推導出f(x)的單調區間.(2)由x∈[1,e],知當a≤1時,f'(x)≥0,故f(x)min=f(1)=a=1;當a≥e時,f'(x)≤0,推導出a=0(舍去);當1<a<e時,推導出a=1(舍去).綜上所述,a=1.(3)f(x)<
(x>0),能推導出f(x)的單調區間.(2)由x∈[1,e],知當a≤1時,f'(x)≥0,故f(x)min=f(1)=a=1;當a≥e時,f'(x)≤0,推導出a=0(舍去);當1<a<e時,推導出a=1(舍去).綜上所述,a=1.(3)f(x)< ![]() x在(1,+∞)上恒成立a<
x在(1,+∞)上恒成立a< ![]() ﹣xlnx在(1,+∞)上恒成立.
﹣xlnx在(1,+∞)上恒成立. ![]() ,g'(x)=x﹣lnx﹣1.h(x)=x﹣lnx﹣1,h'(x)=1﹣
,g'(x)=x﹣lnx﹣1.h(x)=x﹣lnx﹣1,h'(x)=1﹣ ![]() .由此進行分類討論,能求出實數a的取值范圍.
.由此進行分類討論,能求出實數a的取值范圍.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:高中數學 來源: 題型:
【題目】從1開始的自然數按如圖所示的規則排列,現有一個三角形框架在圖中上下或左右移動,使每次恰有九個數在此三角形內,則這九個數的和可以為( )
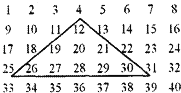
A.2097 B.2112 C.2012 D.2090
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是二次函數,且f(0)=0,f(x+1)=f(x)+x+1,
(1)求f(x)的表達式;
(2)若f(x)>a在x∈[﹣1,1]恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知復數Z1 , Z2在復平面內對應的點分別為A(﹣2,1),B(a,3).
(1)若|Z1﹣Z2|= ![]() ,求a的值.
,求a的值.
(2)復數z=Z1Z2對應的點在二、四象限的角平分線上,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三次函數f(x)=x3+bx2+cx+d(a,b,c∈R)過點(3,0),且函數f(x)在點(0,f(0))處的切線恰好是直線y=0.
(1)求函數f(x)的解析式;
(2)設函數g(x)=9x+m﹣1,若函數y=f(x)﹣g(x)在區間[﹣2,1]上有兩個零點,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩支排球隊進行比賽,約定先勝3局者獲得比賽的勝利,比賽隨即結束.除第五局甲隊獲勝的概率是![]() 外,其余每局比賽甲隊獲勝的概率都是
外,其余每局比賽甲隊獲勝的概率都是![]() .假設各局比賽結果相互獨立.
.假設各局比賽結果相互獨立.
(1)分別求甲隊以3:0,3:1,3:2獲勝的概率;
(2)若比賽結果為3:0或3:1,則勝利方得3分、對方得0分;若比賽結果為3:2,則勝利方得2分、對方得1分.求甲隊得分X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 是自然對數的底數,
是自然對數的底數, ![]() .
.
(1)求![]() 的單調區間,最大值;
的單調區間,最大值;
(2)討論關于x的方程![]() 根的個數.
根的個數.
所以當![]() 時,方程有兩個根;
時,方程有兩個根;
當![]() 時,方程有一兩個根;
時,方程有一兩個根;
當![]() 時,方程有無兩個根.
時,方程有無兩個根.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com