
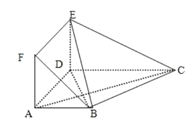
【題目】在多面體![]() 中,底面
中,底面![]() 是梯形,四邊形
是梯形,四邊形![]() 是正方形,
是正方形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,
,![]() .
.![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)設![]() 為線段
為線段![]() 上一點,
上一點,![]() ,試問在線段
,試問在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,若存在,試指出點
,若存在,試指出點![]() 的位置;若不存在,說明理由?
的位置;若不存在,說明理由?
(3)在(2)的條件下,求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)見解析.(2)見解析.(3)![]() .
.
【解析】
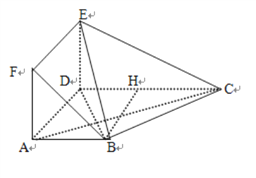
分析:(1)在梯形![]() 中,過點作
中,過點作![]() 作
作![]() 于
于![]() ,可得
,可得![]() ,所以
,所以![]() ,由面
,由面![]() 面
面![]() ,可得出
,可得出![]() ,利用線面垂直的判定定理得
,利用線面垂直的判定定理得![]() 平面
平面![]() ,進而可得平面
,進而可得平面![]() 平面
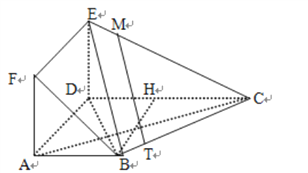
平面![]() ;(2)在線段
;(2)在線段![]() 上取點
上取點![]() ,使得
,使得![]() ,連接
,連接![]() ,先證明
,先證明![]() 與
與![]() 相似,于是得
相似,于是得![]() ,由線面平行的判定定理可得結果;(3)點
,由線面平行的判定定理可得結果;(3)點![]() 到平面
到平面![]() 的距離就是點
的距離就是點![]() 到平面
到平面![]() 的距離,設
的距離,設![]() 到平面
到平面![]() 的距離為
的距離為![]() ,利用體積相等可得,
,利用體積相等可得,![]() ,解得
,解得![]() .
.
詳解:(1)因為面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,![]() ,所以
,所以![]() 面
面![]() ,
,![]() .
.
故四邊形![]() 是正方形,所以
是正方形,所以![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() .
.![]() ,
,
∴![]() ,∴
,∴![]() ∴
∴![]() .
.
因為![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)在線段![]() 上存在點
上存在點![]() ,使得
,使得![]() 平面
平面![]()
在線段![]() 上取點
上取點![]() ,使得
,使得![]() ,連接
,連接![]() .
.
在![]() 中,因為
中,因為![]() ,所以
,所以![]() 與
與![]() 相似,所以
相似,所以![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(3)點![]() 到平面
到平面![]() 的距離就是點
的距離就是點![]() 到平面
到平面![]() 的距離,設
的距離,設![]() 到平面
到平面![]() 的距離為
的距離為![]() ,利用同角相等可得,
,利用同角相等可得,![]() ,可得
,可得![]() .
.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案科目:高中數學 來源: 題型:
【題目】現對某市工薪階層關于“樓市限購令”的態度進行調查,隨機抽調了50人,他們月收入的頻數分布及對“樓市限購令”贊成人數如下表.
月收入(單位百元) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上統計數據填下面2×2列聯表,并問是否有99%的把握認為“月收入以5500元為分界點對“樓市限購令”的態度有差異;
月收入不低于55百元的人數 | 月收入低于55百元的人數 | 合計 | |
贊成 | a=______________ | c=______________ | ______________ |
不贊成 | b=______________ | d=______________ | ______________ |
合計 | ______________ | ______________ | ______________ |
(2)試求從年收入位于![]() (單位:百元)的區間段的被調查者中隨機抽取2人,恰有1位是贊成者的概率。
(單位:百元)的區間段的被調查者中隨機抽取2人,恰有1位是贊成者的概率。
參考公式: ,其中
,其中![]() .
.
參考值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數集![]() 具有性質
具有性質![]() ;對任意的
;對任意的![]() 、
、![]() ,
,![]() ,與
,與![]() 兩數中至少有一個屬于
兩數中至少有一個屬于![]() .
.
(1)分別判斷數集![]() 與
與![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(2)證明:![]() ,且
,且![]() ;
;
(3)當![]() 時,若
時,若![]() ,求集合
,求集合![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,若存在距離為
,若存在距離為![]() 的兩條直線
的兩條直線![]() 和
和![]() ,使得對任意的
,使得對任意的![]() 都有
都有![]() ,則稱函數
,則稱函數![]() 有一個寬為
有一個寬為![]() 的通道.給出下列函數:①
的通道.給出下列函數:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中在區間
.其中在區間![]() 上通道寬度為1的函數由__________ (寫出所有正確的序號).
上通道寬度為1的函數由__________ (寫出所有正確的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸非負半軸為極軸建立極坐標系.
軸非負半軸為極軸建立極坐標系.
(1)寫出曲線C的極坐標方程;
(2)設點M的極坐標為![]() ,過點M的直線
,過點M的直線![]() 與曲線C交于A、B兩點,若
與曲線C交于A、B兩點,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家放開二胎政策后,不少家庭開始生育二胎,隨機調查110名性別不同且為獨生子女的高中生,其中同意生二胎的高中生占隨機調查人數的![]() ,統計情況如下表:
,統計情況如下表:
同意 | 不同意 | 合計 | |
男生 |
| 20 | |
女生 | 20 |
| |
合計 | 110 |
(l)求![]() ,
,![]() 的值
的值
(2)根據以上數據,能否有99%的把握認為同意生二胎與性別有關?請說明理由.
附:![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為![]() ,以原點
,以原點![]() 為極點,以
為極點,以![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的極坐標方程和直線
的極坐標方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,與直線
兩點,與直線![]() 交于
交于![]() 點,射線
點,射線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com