【題目】已知橢圓
上的焦點為
，離心率為
．
（1）求橢圓方程；
（2）設過橢圓頂點
，斜率為
的直線交橢圓于另一點
，交
軸于點
，且
， 
， 
成等比數列，求
的值．
狀元及第系列答案
同步奧數系列答案科目：高中數學 來源： 題型：
【題目】某地區業余足球運動員共有15000人，其中男運動員9000人，女運動員6000人，為調查該地區業余足球運動員每周平均踢足球占用時間的情況，采用分層抽樣的方法，收集300位業務足球運動員每周平均踢足球占用時間的樣本數據（單位：小時）
得到業余足球運動員每周平均踢足球所占用時間的頻率分布直方圖（如圖所示），其中樣本數據分組區間為：（0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]．
將“業務運動員的每周平均踢足球時間所占用時間超過4小時”
定義為“熱愛足球”．
附：K2= 
P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
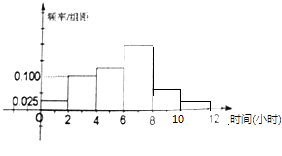
（1）應收集多少位女運動員樣本數據？
（2）估計該地區每周平均踢足球所占用時間超過4個小時的概率．
（3）在樣本數據中，有80位女運動員“熱愛足球”．請畫出“熱愛足球與性別”列聯表，并判斷是否有99%的把握認為“熱愛足球與性別有關”．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，已知曲線C1：ρ=2cosθ，將曲線C1上的點向左平移一個單位，然后縱坐標不變，橫坐標伸長到原來的2倍，得到曲線C，又已知直線l：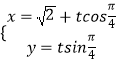 
（t是參數），且直線l與曲線C交于A，B兩點．
（1）求曲線C的直角坐標方程，并說明它是什么曲線；
（2）設定點P（ 
，0），求|PA|+|PB|．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC為銳角三角形，命題p：不等式logcosC 
＞0恒成立，命題q：不等式logcosC 
＞0恒成立，則復合命題p∨q、p∧q、￢p中，真命題的個數為（ ）
A.0
B.1
C.2
D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
為偶函數，且函數
圖象的兩相鄰對稱軸間的距離為
.
（1）求
的值；
（2）求函數
的對稱軸方程；
（3）當
時，方程
有兩個不同的實根，求m的取值范圍。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】經過市場調查，超市中的某種小商品在過去的近40天的日銷售量（單位：件）與價格（單位：元）為時間
（單位：天）的函數，且日銷售量近似滿足
，價格近似滿足
。
(1)寫出該商品的日銷售額
（單位：元）與時間（
）的函數解析式并用分段函數形式表示該解析式（日銷售額=銷售量
商品價格）；
(2)求該種商品的日銷售額的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
