Question

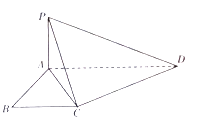
【題目】如圖，已知 是直角梯形， ， ， ， ， 平面 ．

（Ⅰ） 上是否存在點 使 平面 ，若存在，指出 的位置并證明，若不存在，請說明理由；（Ⅱ）證明： ；
（Ⅲ）若 ，求點 到平面 的距離．

Answer 1

【答案】解：（Ⅰ）當 為 中點時滿足題意理由如下：
取 的中點為 ，連結 ．

∵ ， ，∴ ，且 ，∴四邊形 是平行四邊形，即 ．
∵ 平面 ，∴ 平面 ．
∵ 分別是 的中點，∴ ，∵ 平面 ，∴ 平面 ．
∵ ，∴平面 平面 ．
∵ 平面 ，∴ 平面 ．
（Ⅱ）由已知易得 ， ．
∵ ，
∴ ，即 ．
又∵ 平面 ， 平面 ，
∴ ．
∵ ，
∴ 平面
∵ 平面 ，
∴ ．
（Ⅲ）由已知得 ，所以 ．
又 ，則 ，由 得 ，
∵ ，∴ 到平面 的距離為 ．
【解析】(1)根據題意作出輔助線結合已知條件即可得證四邊形 B C D F 是平行四邊形即 B F / / C D，由線面平行的判定定理即可得證B F / / 平面 P C D，再由線面平行的性質定理得到 E F / / P D以及 E F / / 平面 P C D ，利用面面平行的判定定理即可得證平面 B E F / / 平面 P C D從而得證 B E / / 平面 P C D。(2)根據題意結合已知條件代入數值到三棱錐的體積公式求出結果即可。