【題目】下列結(jié)論：
“直線l與平面
平行”是“直線l在平面外”的充分不必要條件；
若p：
，
，則
：
，
；
命題“設(shè)a，
，若
，則
或
”為真命題；
“
”是“函數(shù)
在
上單調(diào)遞增”的充要條件．
其中所有正確結(jié)論的序號為______．
【答案】
【解析】
由線面的位置關(guān)系，結(jié)合充分必要條件的定義可判斷
；由特稱命題的否定為全稱命題，可判斷
；由原命題和逆否命題互為等價命題，可判斷
；由導(dǎo)數(shù)大于等于0恒成立，結(jié)合充分必要條件的定義，可判斷
．
“直線l與平面
平行”可推得“直線l在平面外”，反之，不成立，直線l可能與平面相交，故“直線l與平面平行”是“直線l在平面外”的充分不必要條件，故正確；
若p：
，
，則
：
，
，故錯誤；
命題“設(shè)a，
，若
，則
或
”的逆否命題為
“設(shè)a，，若
且
，則
”，即為真命題，故正確；
函數(shù)
在
上單調(diào)遞增，可得
在恒成立，即有
的最小值，可得
，“
”是“函數(shù)在上單調(diào)遞增”的充分不必要條件，故錯誤．
故答案為：．
閱讀快車系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知直線l：x＋2y－2＝0.
（1）求直線l1：y＝x－2關(guān)于直線l對稱的直線l2的方程；
（2）求直線l關(guān)于點A(1,1)對稱的直線方程．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標系
中，直線
，
.
(1)直線
是否過定點？若過定點，求出該定點坐標，若不過定點，請說明理由;
(2)已知點
，若直線上存在點
滿足條件
，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在直角梯形
中， 
， 
， 
平面
， 
， 
， 
的中點為
．
（
）求證： 
面
．
（
）求證：平面
平面
．
（
）當(dāng)
為何值時，能使
？請給出證明．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)
是由一平面內(nèi)的
個向量組成的集合．若
，且
的模不小于
中除
外的所有向量和的模．則稱
是
的極大向量.有下列命題：
①若
中每個向量的方向都相同，則
中必存在一個極大向量；
②給定平面內(nèi)兩個不共線向量
，在該平面內(nèi)總存在唯一的平面向量
，使得
中的每個元素都是極大向量；
③若
中的每個元素都是極大向量，且
中無公共元素，則
中的每一個元素也都是極大向量．
其中真命題的序號是_______________．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】搶“微信紅包”已經(jīng)成為中國百姓歡度春節(jié)時非常喜愛的一項活動．小明收集班內(nèi)20名同學(xué)今年春節(jié)期間搶到紅包金額
（元）如下（四舍五入取整數(shù)）：
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
對這20個數(shù)據(jù)進行分組，各組的頻數(shù)如下：
（Ⅰ）寫出m，n的值，并回答這20名同學(xué)搶到的紅包金額的中位數(shù)落在哪個組別；
（Ⅱ）記C組紅包金額的平均數(shù)與方差分別為
、
，E組紅包金額的平均數(shù)與方差分別為
、
，試分別比較
與
、
與
的大小；（只需寫出結(jié)論）
（Ⅲ）從A，E兩組所有數(shù)據(jù)中任取2個，求這2個數(shù)據(jù)差的絕對值大于100的概率．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】假設(shè)關(guān)于某設(shè)備的使用年限
和所支出的維修費用
（萬元）有如下的統(tǒng)計資料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
維修費用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由資料知對呈線性相關(guān)關(guān)系．
（1）請畫出上表數(shù)據(jù)的散點圖；
（2）請根據(jù)最小二乘法求出線性回歸方程
的回歸系數(shù)
．
（3）估計使用年限為10年時，維修費用是多少？
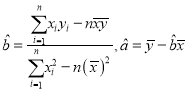
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
