【題目】已知函數f（x）=m﹣|2﹣x|，且f（x+2）＞0的解集為（﹣1，1）．
（1）求m的值；
（2）若正實數a，b，c，滿足a+2b+3c=m．求 
的最小值．
【答案】
（1）解：因為f（x+2）=m﹣|x|
所以由f（x+2）＞0得|x|＜m
由|x|＜m有解，得m＞0，且其解集為（﹣m，m）
又不等式f（x+2）＞0解集為（﹣1，1），故m=1
（2）解：由（1）知a+2b+3c=1，又a，b，c是正實數，
由柯西不等式得 
當且僅當 
時取等號
故 
的最小值為9．
【解析】（1）由f（x+2）＞0得|x|＜m，求出解集，利用f（x+2）＞0的解集為（﹣1，1），求m的值；（2）由（1）知a+2b+3c=1，利用柯西不等式即可求 的最小值．
【考點精析】掌握二維形式的柯西不等式是解答本題的根本，需要知道二維形式的柯西不等式：
當且僅當
時，等號成立．
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，以原點O為極點，x軸的非負半軸為極軸，建立極坐標系，若直線l的參數方程為 
（t為參數，α為l的傾斜角），曲線E的極坐標方程為ρ=4sinθ．射線θ=β，θ=β+ 
，θ=β﹣ 與曲線E分別交于不同于極點的三點A、B、C．
（1）求證：|OB|+|OC|= 
|OA|；
（2）當β= 
時，直線l過B、C兩點，求y0與α的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于下列說法正確的是（ ）
A.若f（x）是奇函數，則f（x）是單調函數
B.命題“若x2﹣x﹣2=0，則x=1”的逆否命題是“若x≠1，則x2﹣x﹣2=0”
C.命題p：?x∈R，2x＞1024，則￢p：?x0∈R， 
D.命題“?x∈（﹣∞，0），2x＜x2”是真命題
查看答案和解析>>
科目：高中數學 來源： 題型：
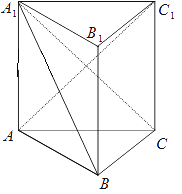
【題目】如圖，三棱柱ABC﹣A1B1C1中，AA1⊥平面ABC，AA1=AC=2BC，∠ACB=90°．
（Ⅰ）求證：AC1⊥A1B；
（Ⅱ）求直線AB與平面A1BC所成角的正切值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖長方體
中，
，
分別為棱
，
的中點
（1）求證:平面
平面
；
（2）請在答題卡圖形中畫出直線
與平面
的交點
（保留必要的輔助線），寫出畫法并計算
的值（不必寫出計算過程）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分
分）
已知圓
，過點
作直線
交圓
于
、
兩點．
（Ⅰ）當
經過圓心
時，求直線
的方程．
（Ⅱ）當直線
的傾斜角為
時，求弦
的長．
（Ⅲ）求直線
被圓
截得的弦長
時，求以線段
為直徑的圓的方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
