【題目】某校為了了解
兩班學(xué)生寒假期間觀看《中國詩詞大會》的時長，分別從這兩個班中隨機抽取5名學(xué)生進行調(diào)查，將他們觀看的時長（單位：小時）作為樣本，繪制成莖葉圖如圖所示（圖中的莖表示十位數(shù)字，葉表示個位數(shù)字）．
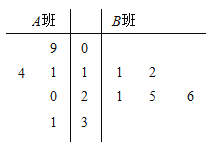
（1）分別求出圖中所給兩組樣本數(shù)據(jù)的平均值，并據(jù)此估計哪個班的學(xué)生平均觀看的時間較長；
（2）從
班的樣本數(shù)據(jù)中隨機抽取一個不超過19的數(shù)據(jù)記為
，從
班的樣本數(shù)據(jù)中隨機抽取一個不超過21的數(shù)據(jù)記為
，求
的概率．
【答案】（1）
班學(xué)生平均觀看時間較長；（2）
.
【解析】試題分析: （1）先根據(jù)平均數(shù)等于總數(shù)除以樣本個數(shù)，計算兩班平均值，再比較大小即可，（2）利用枚舉法計算樣本總數(shù)為9種，再從中計算滿足
的樣本數(shù)，最后根據(jù)古典概型概率公式求概率.
試題解析:（1）
班樣本數(shù)據(jù)的平均值為
由此估計班學(xué)生平均觀看時間大約為17小時，
班樣本數(shù)據(jù)的平均值為
，
由此估計班學(xué)生平均觀看時間較長.
（2）班的樣本數(shù)據(jù)中不超過19的數(shù)據(jù)
有3個，分別為：9,11,14，
班的樣本數(shù)據(jù)中不超過21的數(shù)據(jù)
有3個，分別為：11,12,21，
從班和班的樣本數(shù)據(jù)中各隨機抽取一個共有9種不同情況，分別為：
其中的情況有
兩種，
故的概率為
.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某市需對某環(huán)城快速車道進行限速，為了調(diào)研該道路車速情況，于某個時段隨機對
輛車的速度進行取樣，測量的車速制成如下條形圖：
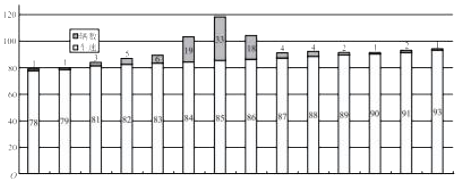
經(jīng)計算：樣本的平均值
，標(biāo)準(zhǔn)差
，以頻率值作為概率的估計值.已知車速過慢與過快都被認(rèn)為是需矯正速度，現(xiàn)規(guī)定車速小于
或車速大于
是需矯正速度.
（1）從該快速車道上所有車輛中任取
個，求該車輛是需矯正速度的概率；
（2）從樣本中任取
個車輛，求這
個車輛均是需矯正速度的概率；
（3）從該快速車道上所有車輛中任取
個，記其中是需矯正速度的個數(shù)為
，求
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某少數(shù)民族的刺繡有著悠久的歷史，下圖
為她們刺繡最簡單的四個圖案，這些圖案都由小正方形構(gòu)成，小正方形數(shù)越多刺繡越漂亮，現(xiàn)按同樣的規(guī)律刺繡（小正方形的擺放規(guī)律相同），設(shè)第n個圖形包含
個小正方形.
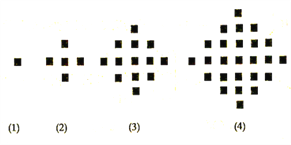
（1）求出
；
（2）利用合情推理的“歸納推理思想”歸納出
與的關(guān)系式，
（3）根據(jù)你得到的關(guān)系式求的表達式
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某商品上市30天內(nèi)每件的銷售價格
元與時間
天函數(shù)關(guān)系是
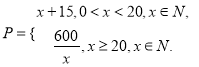該商品的日銷售量
件與時間
天函數(shù)關(guān)系是
.（1）求該商品上市第20天的日銷售金額；
（2）求這個商品的日銷售金額的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）當(dāng)
時，判斷函數(shù)
的單調(diào)性；
（2）若存在
，使得
（
是自然對數(shù)的底數(shù)），求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
(其中
為常數(shù)，
).（Ⅰ）求函數(shù)
的單調(diào)區(qū)間；（Ⅱ）當(dāng)
時，是否存在實數(shù)，使得當(dāng)
時，不等式
恒成立？如果存在，求的取值范圍；如果不存在，請說明理由(其中
是自然對數(shù)的底數(shù)，
).
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】鹽化某廠決定采用以下方式對某塊鹽池進行開采：每天開采的量比上一天減少
，10天后總量變?yōu)樵瓉淼囊话耄瑸榱司S持生態(tài)平衡，剩余總量至少要保留原來的
，已知到今天為止，剩余的總量是原來的
．
（1）求
的值；
（2）到今天為止，工廠已經(jīng)開采了幾天？
（3）今后最多還能再開采多少天？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖所示，已知三棱錐P-ABC，∠ACB=90°，CB=4，AB=20，D為AB的中點，且△PDB是正三角形，PA⊥PC.
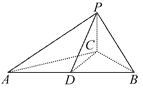
(1)求證：平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
