
【題目】已知函數f(x)=sin(x+θ)+acos(x+2θ),其中a∈R,θ∈(﹣ ![]() ,
, ![]() )
)
(1)當a= ![]() ,θ=
,θ= ![]() 時,求f(x)在區間[0,π]上的最大值與最小值;
時,求f(x)在區間[0,π]上的最大值與最小值;
(2)若f( ![]() )=0,f(π)=1,求a,θ的值.
)=0,f(π)=1,求a,θ的值.
【答案】
(1)解:當a= ![]() ,θ=
,θ= ![]() 時,f(x)=sin(x+θ)+acos(x+2θ)
時,f(x)=sin(x+θ)+acos(x+2θ)
=sin(x+ ![]() )+
)+ ![]() cos(x+
cos(x+ ![]() )=
)= ![]() sinx+
sinx+ ![]() cosx﹣
cosx﹣ ![]() sinx=﹣
sinx=﹣ ![]() sinx+
sinx+ ![]() cosx
cosx
=sin( ![]() ﹣x)=﹣sin(x﹣
﹣x)=﹣sin(x﹣ ![]() ).
).
∵x∈[0,π],∴x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴sin(x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
∴﹣sin(x﹣ ![]() )∈[﹣1,
)∈[﹣1, ![]() ],
],
故f(x)在區間[0,π]上的最小值為﹣1,最大值為 ![]()
(2)解:∵f(x)=sin(x+θ)+acos(x+2θ),a∈R,θ∈(﹣ ![]() ,
, ![]() ),
),
f( ![]() )=0,f(π)=1,
)=0,f(π)=1,
∴cosθ﹣asin2θ=0 ①,﹣sinθ﹣acos2θ=1 ②,
由①求得sinθ= ![]() ,由②可得cos2θ=
,由②可得cos2θ= ![]() =﹣
=﹣ ![]() ﹣
﹣ ![]() .
.
再根據cos2θ=1﹣2sin2θ,可得﹣ ![]() ﹣
﹣ ![]() =1﹣2×
=1﹣2× ![]() ,
,
求得 a=﹣1,∴sinθ=﹣ ![]() ,θ=﹣
,θ=﹣ ![]() .
.
綜上可得,所求的a=﹣1,θ=﹣ ![]()
【解析】(1)由條件利用兩角和差的正弦公式、余弦公式化簡函數的解析式為f(x)=﹣sin(x﹣ ![]() ),再根據x∈[0,π],利用正弦函數的定義域和值域求得函數的最值.(2)由條件可得θ∈(﹣
),再根據x∈[0,π],利用正弦函數的定義域和值域求得函數的最值.(2)由條件可得θ∈(﹣ ![]() ,
, ![]() ),cosθ﹣asin2θ=0 ①,﹣sinθ﹣acos2θ=1 ②,由這兩個式子求出a和θ的值.
),cosθ﹣asin2θ=0 ①,﹣sinθ﹣acos2θ=1 ②,由這兩個式子求出a和θ的值.
【考點精析】解答此題的關鍵在于理解兩角和與差的余弦公式的相關知識,掌握兩角和與差的余弦公式:![]() ,以及對兩角和與差的正弦公式的理解,了解兩角和與差的正弦公式:
,以及對兩角和與差的正弦公式的理解,了解兩角和與差的正弦公式:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】從某市統考的學生數學考試卷中隨機抽查100份數學試卷作為樣本,分別統計出這些試卷總分,由總分得到如下的頻率分別直方圖.
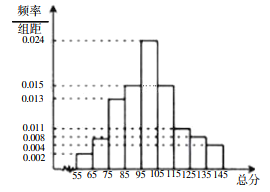
(1)求這100份數學試卷成績的中位數;
(2)從總分在![]() 和
和![]() 的試卷中隨機抽取2份試卷,求抽取的2份試卷中至少有一份總分少于65分的概率.
的試卷中隨機抽取2份試卷,求抽取的2份試卷中至少有一份總分少于65分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關命題的說法正確的是( )
A. “若x>1,則2x>1”的否命題為真命題
B. “若cosβ=1,則sinβ=0”的逆命題是真命題
C. “若平面向量a,b共線,則a,b方向相同”的逆否命題為假命題
D. 命題“若x>1,則x>a”的逆命題為真命題,則a>0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知雙曲線C: ![]() ﹣y2=1(a>0)的右焦點為F,點A,B分別在C的兩條漸近線AF⊥x軸,AB⊥OB,BF∥OA(O為坐標原點).
﹣y2=1(a>0)的右焦點為F,點A,B分別在C的兩條漸近線AF⊥x軸,AB⊥OB,BF∥OA(O為坐標原點). 
(1)求雙曲線C的方程;
(2)過C上一點P(x0 , y0)(y0≠0)的直線l: ![]() ﹣y0y=1與直線AF相交于點M,與直線x=
﹣y0y=1與直線AF相交于點M,與直線x= ![]() 相交于點N.證明:當點P在C上移動時,
相交于點N.證明:當點P在C上移動時, ![]() 恒為定值,并求此定值.
恒為定值,并求此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,為保護河上古橋OA,規劃建一座新橋BC,同時設立一個圓形保護區,規劃要求:新橋BC與河岸AB垂直;保護區的邊界為圓心M在線段OA上并與BC相切的圓,且古橋兩端O和A到該圓上任意一點的距離均不少于80m,經測量,點A位于點O正北方向60m處,點C位于點O正東方向170m處(OC為河岸),tan∠BCO= ![]() .
. 
(1)求新橋BC的長;
(2)當OM多長時,圓形保護區的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業有甲、乙兩個研發小組,他們研發新產品成功的概率分別為 ![]() 和
和 ![]() .現安排甲組研發新產品A,乙組研發新產品B,設甲、乙兩組的研發相互獨立.
.現安排甲組研發新產品A,乙組研發新產品B,設甲、乙兩組的研發相互獨立.
(1)求至少有一種新產品研發成功的概率;
(2)若新產品A研發成功,預計企業可獲利潤120萬元;若新產品B研發成功,預計企業可獲利潤100萬元,求該企業可獲利潤的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某輪船公司的一艘輪船每小時花費的燃料費與輪船航行速度的平方成正比,比例系數為![]() 輪船的最大速度為15海里
輪船的最大速度為15海里![]() 小時
小時![]() 當船速為10海里
當船速為10海里![]() 小時,它的燃料費是每小時96元,其余航行運作費用(不論速度如何)總計是每小時150元
小時,它的燃料費是每小時96元,其余航行運作費用(不論速度如何)總計是每小時150元![]() 假定運行過程中輪船以速度v勻速航行.
假定運行過程中輪船以速度v勻速航行.
![]() 求k的值;
求k的值;
![]() 求該輪船航行100海里的總費用
求該輪船航行100海里的總費用![]() 燃料費
燃料費![]() 航行運作費用
航行運作費用![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com