
【題目】已知函數![]() .
.
(1)求函數![]() 的定義域;
的定義域;
(2)判斷函數![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(3)若函數![]() ,求函數
,求函數![]() 的零點.
的零點.
【答案】(1) ![]() (2)
(2) ![]() 為奇函數(3)
為奇函數(3)![]()
【解析】試題分析:(1)要使函數![]() 有意義,
有意義, ![]() 必須滿足
必須滿足![]() ,從而得到定義域;(2)利用奇偶性定義判斷奇偶性;(3)函數
,從而得到定義域;(2)利用奇偶性定義判斷奇偶性;(3)函數![]() 的零點即方程
的零點即方程![]() 的根.即
的根.即![]() 的根,又
的根,又![]() 為奇函數,所以
為奇函數,所以![]() .易證:
.易證: ![]() 在定義域
在定義域![]() 上為增函數,∴由
上為增函數,∴由![]() 得
得![]() ,從而解得函數
,從而解得函數![]() 的零點.
的零點.
試題解析:
(1)要使函數![]() 有意義,
有意義, ![]() 必須滿足
必須滿足![]() ,∴
,∴![]() ,
,
因此, ![]() 的定義域為
的定義域為![]() .
.
(2)函數![]() 為奇函數.
為奇函數.
∵![]() 的定義域為
的定義域為![]() ,對
,對![]() 內的任意
內的任意![]() 有:
有:
![]()
![]() ,
,
所以, ![]() 為奇函數.
為奇函數.
(3)函數![]() 的零點即方程
的零點即方程![]() 的根.即
的根.即![]() 的根,
的根,
又![]() 為奇函數,所以
為奇函數,所以![]() .
.
任取![]() ,且
,且![]() ,
,
![]()
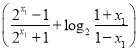
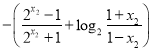

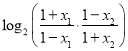
∵![]() ,∴
,∴![]() ,∴
,∴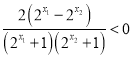
∵![]() 且
且![]() ,∴
,∴![]()
![]() ,
,
∴![]() ,∴
,∴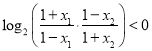 ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() 在定義域
在定義域![]() 上為增函數,
上為增函數,
∴由![]() 得
得![]() 解得
解得![]() 或
或![]() ,
,
驗證當![]() 時,
時, ![]() 不符合題意,當
不符合題意,當![]() 時,符合題意,
時,符合題意,
所以函數![]() 的零點為
的零點為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(2x+b)ex , F(x)=bx﹣lnx,b∈R.
(1)若b<0,且存在區間M,使f(x)和F(x)在區間M上具有相同的單調性,求b的取值范圍;
(2)若F(x+1)>b對任意x∈(0,+∞)恒成立,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,拋物線C:y2=2px(p>0)的焦點為F,經過點F的直線l與拋物線交于P,Q兩點,弦PQ的中點為N,經過點N作y軸的垂線與C的準線交于點T.
(Ⅰ)若直線l的斜率為1,且|PQ|=4,求拋物線C的標準方程;
(Ⅱ)證明:無論p為何值,以線段TN為直徑的圓總經過點F.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)在R上存在導函數f′(x),對于任意的實數x,都有f(x)=4x2﹣f(﹣x),當x∈(﹣∞,0)時,f′(x)+ ![]() <4x,若f(m+1)≤f(﹣m)+4m+2,則實數m的取值范圍是( )
<4x,若f(m+1)≤f(﹣m)+4m+2,則實數m的取值范圍是( )
A.[﹣ ![]() ,+∞)
,+∞)
B.[﹣ ![]() ,+∞)
,+∞)
C.[﹣1,+∞)
D.[﹣2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知Ω={(x,y)|0≤x≤1,0≤y≤1},A是由直線y=0,x=a(0<a≤1)和曲線y=x3圍成的曲邊三角形的平面區域,若向區域Ω上隨機投一點P,點P落在區域A內的概率是 ![]() ,則a的值為( )
,則a的值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了研究年宣傳費![]() (單位:千元)對銷售量
(單位:千元)對銷售量![]() (單位:噸)和年利潤
(單位:噸)和年利潤![]() (單位:千元)的影響,搜集了近 8 年的年宣傳費
(單位:千元)的影響,搜集了近 8 年的年宣傳費![]() 和年銷售量
和年銷售量![]() 數據:
數據:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 38 | 40 | 44 | 46 | 48 | 50 | 52 | 56 |
| 45 | 55 | 61 | 63 | 65 | 66 | 67 | 68 |
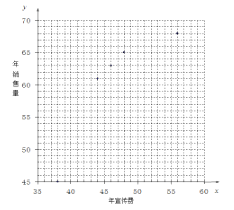
(Ⅰ)請補齊表格中 8 組數據的散點圖,并判斷![]() 與
與![]() 中哪一個更適宜作為年銷售量
中哪一個更適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的函數表達式?(給出判斷即可,不必說明理由)
的函數表達式?(給出判斷即可,不必說明理由)
(Ⅱ)若(Ⅰ)中的![]() ,且產品的年利潤
,且產品的年利潤![]() 與
與![]() ,
, ![]() 的關系為
的關系為![]() ,為使年利潤值最大,投入的年宣傳費 x 應為何值?
,為使年利潤值最大,投入的年宣傳費 x 應為何值?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com